1. Reference problem#
1.1. Geometry#
The test cases simulate a polycrystal law on a representative elementary volume (VER) which is a cube sample of 10x10x10. The cube (figure 1) sample has been generated thanks to Dream3D software. The Dream3D output files have been converted into code_aster format thanks to the python script called LengMorph developed by UKC team and Bristol University.
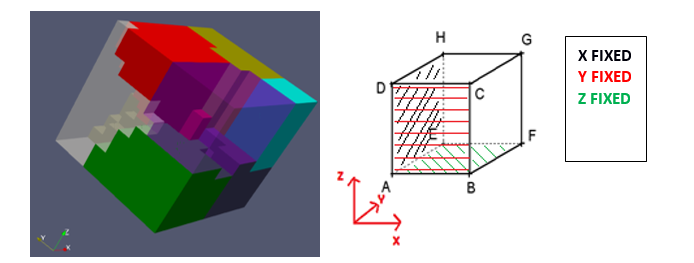
Figure 1. Cube sample generated by DREAM3D — 8 grains orientations
1.2. Material properties#
The sample is composed of 8 to 64 grains with different sizes and different orientations. The properties of each grain are defined in the « Matpreoperies.inc » file which gathers all the necessary parameters to run the crystal plasticity finite element model. There are 175 material parameters of which the most important one are described in the next paragraph.
Description of the relevant material properties: the elastic behaviour is common for all the grains and ruled by the generalized Hooke’s law in cubic symmetry (P1, P2, P3)
\(>\) with \(>\) and \(>\).
Each single crystal has one family of slip system defined by P25. The normal slip plane is the direction [110] is defined by the values (P33, P34, P35). The slip direction is [111] (P36, P37, P38). The parameters from P57 to P70 define the orientation of the grain. The parameters (P73, P97, P98, P99) characterized the different parameters of the flow rule respectively strain rate sensitivity factor n=50, the hardening modulus \(>\), a fitting parameter \(>\), and the critical resolved shear stress, and the critical resolved shear stress \(>\) regarding the hardening law. The P145, P146 states that the resolution is in fully implicit integration in the finite strain nonlinear geometry rather than the small deformation theory. The maximum number of iterations for one-time step is limited to 100 (P154). The Absolute Tolerance on Slip is \(>\). The parameter 156 specifies which hardening law is used, here the power hardening law is used. P157, P158 define the parameters \(>\), \(>\) used in the expression of intragranular stress. The properties of the grain end with the ID number of the grain (P173).
The UMAT law accounts for the length scale of each element.
1.3. Boundary conditions and loads#
All the sample studied have the same type of boundary conditions. This problem is cubic symmetric. There are three orthogonal symmetric plans: (OZX), (OXY), (), (OYZ) and the material properties are identical in the orthogonal directions of these three symmetric plans.
Regarding the figure 7 the faces <ABCD> is fixed on the Y axis, <AEDH> is fixed on X axis, <ABFE> is fixed on Z axis. Finitely the face <EFGH> undergo a ramp displacement toward Y axis until \(>\).
1.4. Description of the tests#
In this testcase the displacement is a ramp that reaches Y µm in a given time. The Von Mises stress field will be computed.
Pre-process
The simulation runs for 1 second. The command file describes the different steps followed by Code-aster. The UMAT law is executed with the native code_aster function make_shared. UMAT file requires 8 files:
param_array.inc: fortran parameters instructions (could be defined directly in the main fortran routine);
orien.inc: orientation of grains;
xvalues.bin, yvalues.bin, zvalues.bin, el_centroid.bin: location of each element and calculation of its length scale;
boundfeat.bin: read boundary feature.
UMAT routine
The UMAT routine accounts for various physical phenomena that are tested in elementary simulations (Models A to D). The time-step has a significant influence on the mechanical response and the convergence of the model due to the relationship between the loading velocity and the time step. In case of larger time steps the simulation can end up with singular matrix errors generated by the UMAT routine itself (LUDCMP subroutine) as shown in Figure 2.

Figure 2: Termination message (up), UMAT script “singular matrix” (down)
To avoid such error, it is proposed to use an optimal constant time-step of 0.0001. This coefficient is a heuristic estimation given the formula (1).
\(>\)
Process
The resolution is performed with STAT_NON_LINE. Note that Abaqus uses « NLGEOM » options (Simo-Miehe large deformations) whilst code_aster uses small deformation.
Post-process
Once University of Bristol and EDF R&D UKC have run the same testcase, it is possible to compare at the same location the differences in stresses and displacement.
The results calculated with POST_ELEM/TEST_TABLE are the average of the Von Mises stress on Gauss Points of a selected element.