1. Reference problem#
1.1. Geometry#
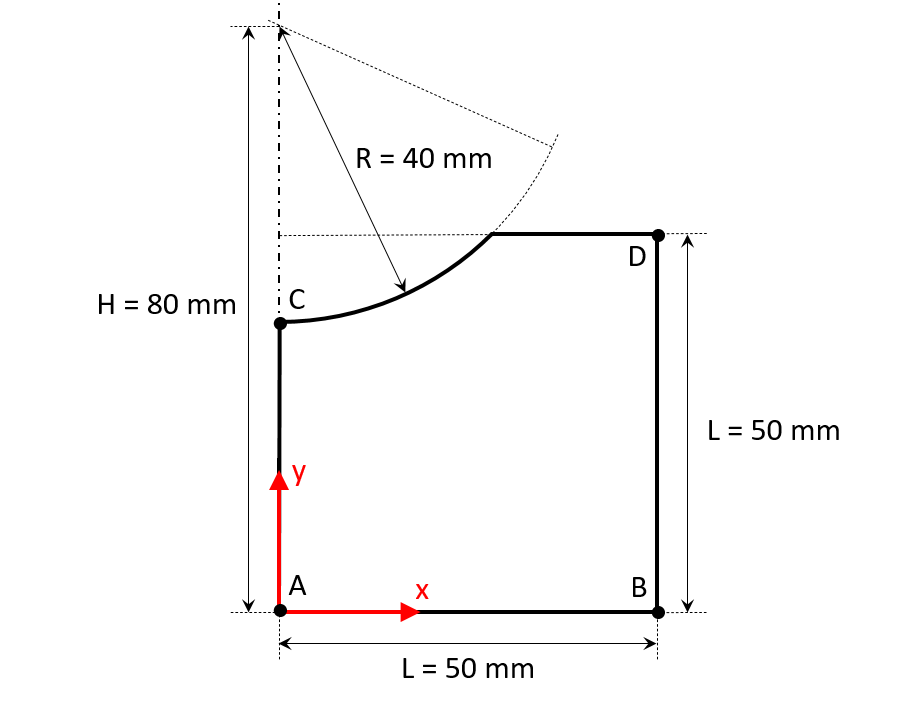
We consider a square plate with a side of 50 mm, the top of which is hollowed out by a disk with a radius of 40 mm whose center is located 80 mm from the bottom of the plate. The geometry is shown in the figure below. The top of the plate (line \(\mathit{CD}\)) is in contact with the corrosive medium.
The case is treated axisymmetrically, which is equivalent to considering a cylinder whose upper face is hollowed out by a sphere.
1.2. Material properties#
The material is Alloy 600 at 350° C. Its behavior is considered to be visco-elastic, non-linear, isotropic.
The elastic properties are:
\(E=200000\mathit{MPa}\)
\(\nu =\mathrm{0,3}\)
The visco-elastic behavior is modelled by a Lemaitre law, whose parameters are:
\(n=\mathrm{3,77}\)
\(m=\mathrm{4,26}\)
\(K(T)=\mathrm{17,67.}\mathrm{exp}(\frac{47500}{\mathrm{8,31}(T+\mathrm{273,15})})\) with \(T\) in °C. For \(T=350°C\), \(K=170182\)
The parameters to be entered in the operator DEFI_MATERIAU under the keyword factor LEMAITRE [U4.43.01] are \(n\), \(1/m\) and \(1/K\).
1.3. Boundary conditions and loads#
Since the case is axisymmetric, the movement along the \(x\) axis on the \(\mathit{AC}\) side is blocked. In order to block rigid modes, the movement along the \(y\) axis of the point \(A\) is blocked.
The loading consists in applying to side \(\mathit{BD}\) a movement of \(\mathrm{0,1}\mathit{mm}\) along the axis \(x\), progressively up to \(t=1h\), then the loading is kept constant until \(t=1000h\).