1. Reference problem

1.1. Geometry

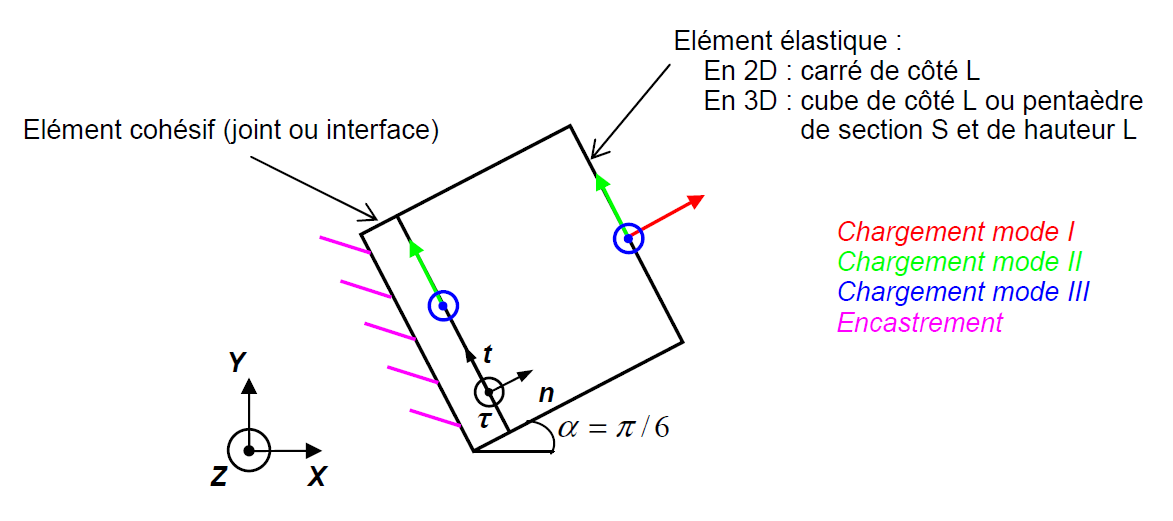
Figure 1: Representation of the system of two elements in plane \((X,Y)\). We choose \(L\mathrm{=}1\mathit{mm}\).

1.1.1. Geometry: case X- FEM

In the models in formulation XFEM, there is no longer a cohesive joint or interface element in the model, but the cohesive law is defined on the interface using the DEFI_CONTACT command, as one would do for a contact law. Consequently, the square is meshed with a few elements and the line of discontinuity is introduced in the middle of the square, in an irregular manner: it intersects elements that are elastic in this case.

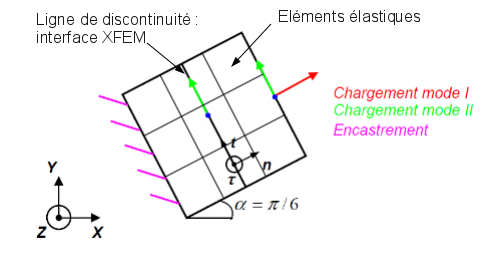
Figure 2: Modeling X- FEM in plane \((X,Y)\). We choose \(L=1\mathrm{mm}\).

1.2. Material properties

1.2.1. Cohesive laws

1.2.1.1. Material RUPT_FRAG

**Cube:* elastic

Young’s module: \(E=0.5\mathrm{MPa}\) (except for J, K and L models where \(E=100\mathrm{MPa}\) is taken, this choice is purely practical)

Poisson’s Ratio \(\nu =0\)

Joint element: laws CZM_EXP_REG, CZM_LIN_REG

Interface element: laws CZM_OUV_MIX, CZM_EXP_MIX,,, CZM_TAC_MIX, CZM_FAT_MIX

Mixed law for linear finite elements: law CZM_LIN_MIX

Critical surface energy density:	\({G}_{c}=0.9N/\mathrm{mm}\)	(keyword: GC)
critical stress:	\({\sigma }_{c}=1.1\mathrm{MPa}\)	(keyword: SIGM_C)
Joint element:
penalization of adherence	PENA_ADHERENCE = \({10}^{-3}\mathrm{mm}\)	(keyword: PENA_ADHERENCE)
(small energy regulation parameter at 0, see [])
criminalization of contact	PENA_CONTACT = 1 (by default)	(keyword: PENA_CONTACT)
Interface element:
Penalization of Lagrangian	PENA_LAGR =100 (by default)	(keyword: PENA_LAGR)
Slip stiffness	RIGI_GLIS =10 (by default)	(keyword: RIGI_GLIS)
Mixed law for linear finite elements:
Penalization of Lagrangian	PENA_LAGR =10	(keyword: PENA_LAGR)

NB: Material data is of course not intended to represent a particular material. They are only intended for numerical validation tests.

1.2.1.2. Material RUPT_DUCT

**Cube:* elastic

Young’s module: \(E={10}^{6}\mathrm{MPa}\) (this choice is purely practical)

Poisson’s Ratio \(\nu =0\)

Interface element: law CZM_TRA_MIX

Critical surface energy density:	\({G}_{c}=0.9N/\mathrm{mm}\)	(keyword: GC)
critical constraint:	\({\sigma }_{c}=9\mathrm{MPa}\)	(keyword: SIGM_C)
Extrinsic form coefficient	\(0.0625\)	(keyword: COEF_EXTR)
Plastic tray form factor	\(0.3125\)	(key word: COEF_PLAS)
Lagrangian penalty	PENA_LAGR =100 (by default)	(keyword: PENA_LAGR)
Slip stiffness	RIGI_GLIS =10 (by default)	(keyword: RIGI_GLIS)

NB: Material data is of course not intended to represent a particular material. They are only intended for numerical validation tests.

1.3. Boundary conditions and loads

Embedment: The imposed displacements are zero on the face of the cohesive element opposite to the elastic element.

In mode \(I\): An imposed displacement

is applied to the face of the elastic element opposite the joint (see FIG. 1).

DX= 2.16506351

DY= 1.250

DZ= 0

In mode \(\mathrm{II}\): Imposed displacement

is applied to all the nodes of the solid element.

DX= -1.250

DY= 2.16506350946110

DZ= 0

In mode \(\mathrm{III}\): Imposed displacement

is applied to all the nodes of the solid element.

DX= 0.0

DY= 0.0

DZ= 2.5

For laws CZM_OUV_MIX, CZM_EXP_MIX and CZM_TAC_MIX, the same vectors normalized to 1 are used.

For fatigue law CZM_FAT_MIX (in \(I\) mode only) the same vectors normalized to \(\mathrm{0,094}\) are used. This value corresponds to the magnitude of the load because this one is multiplied by a cyclic function, zero at zero, which is equal to 1 at odd times and 0 at even times.

For the ductile law CZM_TRA_MIX (in \(I\) mode only) the same vectors normalized to 1 are used. Cyclic loading is applied to test all the states of the law but also monotonic loading. The tests are carried out with the first load.

1.3.1. Loading: case X- FEM

Embed: The movements imposed are zero on the left side of the square.

In mode \(I\): An imposed displacement

is applied to the right side of the square (see figure 2).

DX= 2.16506351

DY= 1.250

DZ= 0