1. Reference problem

1.1. Geometry

The stresses and deformations are homogeneous in the volume element. This can be represented by a plane or a solid element, for example:

1.2. Material properties

Law of elastoplastic behavior with linear kinematic work hardening.

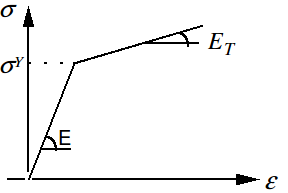
\(\begin{array}{c}E\mathrm{=}195000\mathit{MPa}\\ \nu \mathrm{=}0.3\\ {\sigma }^{Y}\mathrm{=}181\mathit{MPa}\\ {E}_{T}\mathrm{=}1930\mathit{MPa}\end{array}\)

1.3. Boundary conditions and loads

The volume element is locked along \(\mathrm{Ox}\) along the \([\mathrm{2,4}]\) side while being subjected to a pull \({\sigma }^{D}\) and a shear force \({\tau }^{D}\).

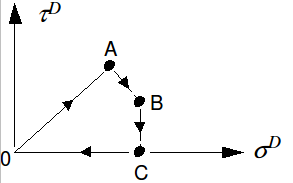
The loading path is as follows:

	\({\sigma }^{D}\)	\({\tau }^{D}\)
	(\(\mathit{MPa}\))	(\(\mathit{MPa}\))
\(A\)	151.2	93.1
\(B\)	257.3	33.1
\(C\)	259.3	0