1. Description

1.1. Geometry

We consider a beam with a length \(10m\), oriented to \(45°\) in the plane \(\mathit{XOZ}\).

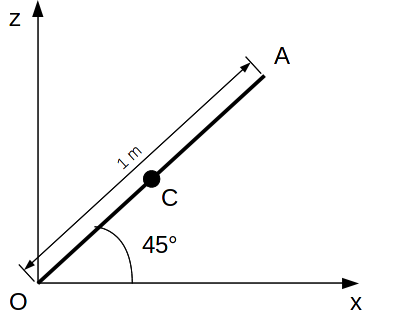
The section of the beam is rectangular, \(\mathrm{0,1}m\) wide, \(\mathrm{0,2}m\) high.

1.2. Material properties

The material uses the following properties:

Young’s module	\({E}_{b}\mathrm{=}1.0E+10\mathit{Pa}\)
Poisson’s Ratio	\({\nu }_{b}\mathrm{=}0.25\)

1.3. Boundary conditions and loads

Node \(O\) is stuck moving in all directions and rotating around \(Y\). Node \(A\) is stuck in motion according to \(Y\). In addition, the beam is forbidden to rotate on itself.

The movements of node \(A\) are imposed as follows: \(\mathit{DX}\mathrm{=}\frac{\mathrm{-}\sqrt{2}}{2}\frac{t}{100}\) and \(\mathit{DZ}\mathrm{=}\frac{\mathrm{-}\sqrt{2}}{2}\frac{t}{100}\) with and with \(t\) taking values from 0 to 1 in increments of \(0.1\).

A force of \(100N\) according to \(Y\) is applied to node \(C\) (center of the beam) so that the beam moves in the direction \(Y\).

1.4. Reference

The reference results are obtained with a non-linear calculation and a beam oriented along the \(X\) axis. For this orientation the value of the spin angle always remains the same during the calculation, with and without re-updating the results are identical.

For the reference, the displacement imposed on node \(A\) is: \(\mathit{DX}\mathrm{=}\mathrm{-}\frac{t}{100}\)

The \(\mathit{DY}\) displacement of node \(C\) (center of the beam) gives the reference value.