1. Reference problem

1.1. Geometry and loading

Consider a hollow cylinder with a length \(L\), an inner radius \({R}_{f}\) and an outer radius \(R\). Let’s say a rigid frame with a circular cross section of radius \({R}_{f}\) embedded in its center. The inner and outer surfaces of the hollow cylinder are denoted \({\Gamma }_{i}\) and \({\Gamma }_{e}\) (see [Figure 1.1-a]). The loading consists in applying, on the rigid frame, a displacement \({U}^{i}{e}_{z}\) (\({U}^{i}>0\)) as well as a zero displacement on the outer edge \({\Gamma }_{e}\).

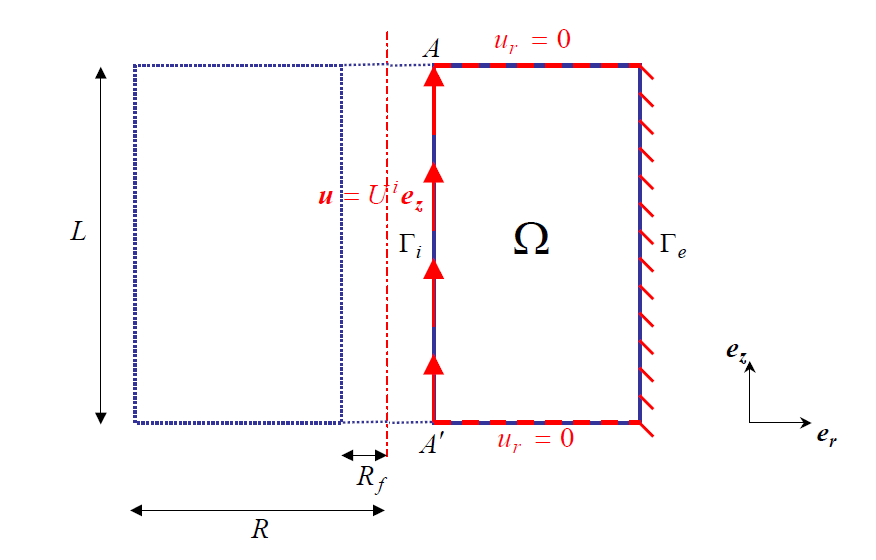
Figure 1.1-a: Domain diagram and load

We hypothesize an axisymmetric solution which allows us to restrict our study to a 2D rectangular domain \(\Omega\). The dimensions of the domain are as follows:

. The load on the rigid frame will be taken into account by applying the imposed displacement

all over the side

of the domain \(\mathrm{2D}\) as well as zero displacement to the side

to take into account the embedment of the cylinder. Finally, a zero radial displacement is imposed on the lower and upper faces of the domain in order to avoid a singularity linked to a change in condition at the limits at the points.

and \(A\text{'}\) (see [Figure 1.1-a]). These boundary conditions will lead to an anti-plane solution (independent of

) which makes it easier to obtain an analytical solution.