1. Reference problem#
1.1. Geometry#
The geometry is chosen deliberately simple, to translate a state of homogeneous stresses and deformations, as is the case in uniaxial traction. This is a volume element represented by a square with side \(\mathrm{0.01mm}\). The modeling is axisymmetric, and the traction takes place with imposed deformation.
1.2. Material properties#
The characteristics set are as follows:
Keyword ELAS:
YOUNG = \(143006.0\mathrm{MPa}\)
NU= \(0.33\)
UN_SUR_M = \(0\)
G2_0= \(0.28\)
The initial values and limits of the parameters to be identified are:
Keyword CIN2_CHAB |
Initial value |
Inf terminal |
Upper terminal |
R0 |
100 |
0.01 |
1000 |
R_I |
120 |
0.01 |
2000 |
B |
0.0934 |
0.01 |
20 |
K |
4.307 |
0.01 |
20 |
W |
0.156 |
0.01 |
20 |
G1_0 |
245 |
0.01 |
2000 |
C1_I |
2628 |
0.01 |
20000 |
C2_I |
105 |
0.01 |
2000000 |
A_I |
1.24 |
0.01 |
2000 |
Keyword LEMAITRE |
|||
UN_SUR_K |
0.003 |
0.00001 |
2000 |
EXP_N |
15 |
0.01 |
2000 |
1.3. Boundary conditions and loads#
\(\mathrm{DY}=0\) on the bottom
\(\mathrm{DX}=0\) on the left side
\(\mathrm{DY}\) imposed on the top, such as:
\(\mathrm{DY}(t)=({\mathrm{EPS}}_{\mathrm{final}}\ast H)/\mathrm{tmax}\ast t\)
With \({\mathrm{EPS}}_{\mathrm{final}}=0.01\)
\(H=0.01\mathrm{mm}\)
\(\mathrm{Tmax}=\mathrm{200s},\mathrm{1000s},\mathrm{2000s},\mathrm{10000s}\)
This corresponds to imposed deformation rates of \({5.10}^{-4}/s,{1.10}^{-3}/s,{5.10}^{-3}/s,{1.10}^{-6}/s\).
1.4. Initial conditions#
Zero stresses and deformations.
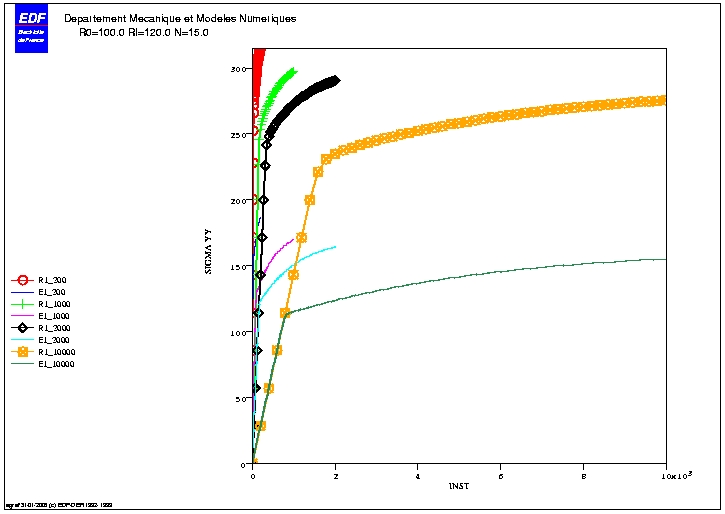
1.5. Reference curves#

The curves obtained with the initial values of the parameters are as follows: