1. Reference problem#

1.1. Geometry and boundary conditions#

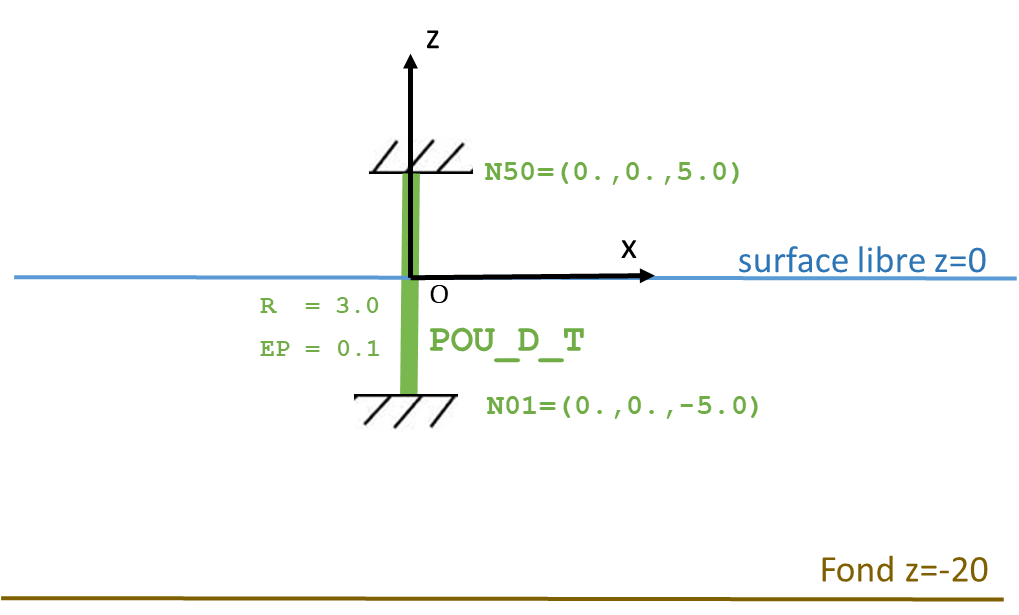
The figure below represents the reference problem: a hollow cylindrical pile with a length \(L=10m\), an external radius \(R=3.0m\) and a thickness \(\mathit{ep}=0.1m\). It is half submerged in a water column of height \(h=20m\). The ends of the battery are recessed.

We note \({S}_{w}=\mathrm{\pi }{R}^{2}\) the hydraulic section (seen by the fluid) transverse to the pile and \(S=\mathrm{\pi }(2.R.\mathit{ep}-{\mathit{ep}}^{2})\) the real cross section.

1.2. Material properties#

The material has isotropic elastic behavior:

Young’s module	\(20000\mathit{GPa}\)
Poisson’s Ratio	\(0.3\)
Battery density \({\rho }_{}\)	\(780\mathit{kg}/{m}^{3}\)
Water density \({\mathrm{\rho }}_{w}\)	\(1000\mathit{kg}/m3\)
Added mass coefficient \({C}_{a}\)	\(1.0\)
Drag coefficient \({C}_{d}\)	\(0.6\)

1.3. Wave kinematics#

We consider a regular monodirectional swell directed along the \(+x\) axis, of order 1 (Airy swell), of height \(H\), of period \(T\) and of wavelength \(\mathrm{\lambda }\), see diagram below.

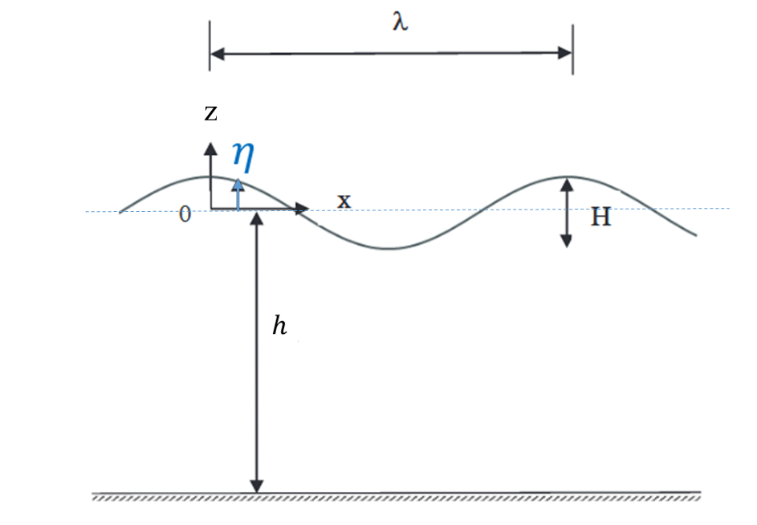
The free surface \(\mathrm{\eta }\) as a function of space \(x\) and time \(t\) is expressed:

(1.1)#\[ \ mathrm {\ eta} (x, t) =\ frac {H} {2}\ mathrm {cos} (kx-\ mathrm {\ omega} t)\]

with \(k=\frac{2\mathrm{\pi }}{\mathrm{\lambda }}\) the wave number and \(\mathrm{\omega }=\frac{2\mathrm{\pi }}{T}\) the pulsation.

The speed of fluid \({V}_{w}=(u,v,w)\) is as follows:

(1.2)#\[\begin{split} \ begin {array} {c} u (x, z, t) =0\\ v (x, z, t) =0\\ v (x, z, t) =\ frac {\ omega}\ frac {\ mathrm {sinh} (k (z, t)} (k (h+z))} {\ mathrm {sinh})}\ mathrm {sin} (k.x-\ mathrm {\ omega} t)\\ w (x, z, t) =\ frac {H} {2}\ mathrm {\ omega}\ frac {\ mathrm {sinh} (k (h+z))}} {\ mathrm {sinh})} {\ mathrm {sinh} (kh)}\ mathrm {sinh} (kh)}\ mathrm {sinh} (kh)}\ mathrm {sinh} (kh)} end {array}\end{split}\]

The acceleration of the fluid is noted \({a}_{w}=\frac{\partial {v}_{w}}{\partial t}\).

1.4. Loads#

The pile is subject to Morison’s efforts induced by a field of regular waves of height \(H=4m\) and period \(T=10s\). Note that Archimedes” thrust is not taken into account in this problem. The weight is imposed but has*a priori* no influence on the solution given the embedding conditions.

Modeling A

The battery is subjected to Morison forces (drag term and inertia terms) in a fluid at rest.

(1.3)#\[ {F} _ {\ text {mor}} =\ frac {1} {2} {2} {2} {C} _ {d} {\ mathrm {\ rho}}} _ {w} _ {w} ({v} _ {w}} ^ {v} _ {w} ^ {v}} ^ {\ text {ortho}}}) ({v} _ {w}} ^ {v} _ {w} ^ {\ text {ortho}} - {v} _ {s}} ^ {\ text {ortho}}}) + {\ mathrm {\ rho}} _ {w} {a} _ {a} _ {w} _ {w} _ {w}} ^ {w} ^ {w} ^ {w} ^ {w} ^ {w} ^ {w} ^ {w} ^ {w} ^ {w} ^ {w} ^ {w} ^ {\ text {ortho}} ^ {\ text {ortho}} ^ {\ text {ortho}} ^ {\ text {ortho}} ^ {\ text {ortho}}} ^ {\ text {ortho}} ^ {\ text {ortho}}} ^ {\ text {ortho}} ^ {\ text {ortho}} ({a} _ {w} ^ {\ text {ortho}}} - {a} _ {s} ^ {\ text {ortho}})\]

where \({v}_{w}\) and \({v}_{s}\) respectively designate the fluid speed and the solid speed (mechanical load input parameter FORCE_POUTRE). The symbol \(\text{ortho}\) represents the projection in the direction normal to the neutral fiber of the beam [1] _ . It should be noted that these are linear forces that are applied in a distributed manner on the beam.

The first term corresponds to the drag force, the second and the third correspond to the inertia terms. Since the acceleration of the solid is zero, these are reduced to the terms relating to fluid acceleration.

Note: Morison’s efforts depend on the position of the beam; they should be mentioned as follower loadings in the calculations.