1. Reference problem#

1.1. Geometry and boundary conditions#

The figure below represents the reference problem: a cylindrical cable immersed under the free surface in a column of water of height \(h=30m\). The ends of the beam are supported by two springs, which are themselves embedded at their ends.

Note \({S}_{w}\) the hydraulic section (seen by the fluid) transverse to the beam.

1.2. Material properties#

The material has an isotropic elastic behavior:

Young’s module	\(200\mathit{GPa}\)
Poisson’s Ratio	\(0.3\)
Cable density \(\mathrm{\rho }\)	\(7800\mathit{kg}/{m}^{3}\)
Water density \({\mathrm{\rho }}_{w}\)	\(1000\mathit{kg}/{m}^{3}\)
Spring stiffness according to x, y and z	\(50.0N/m\)
Drag coefficient \({C}_{d}\)	\(1.0\)

1.3. Wave kinematics#

We consider a regular monodirectional swell directed along the \(+x\) axis, of order 1 (Airy swell), of height \(H\), of period \(T\) and of wavelength \(\mathrm{\lambda }\), see diagram below.

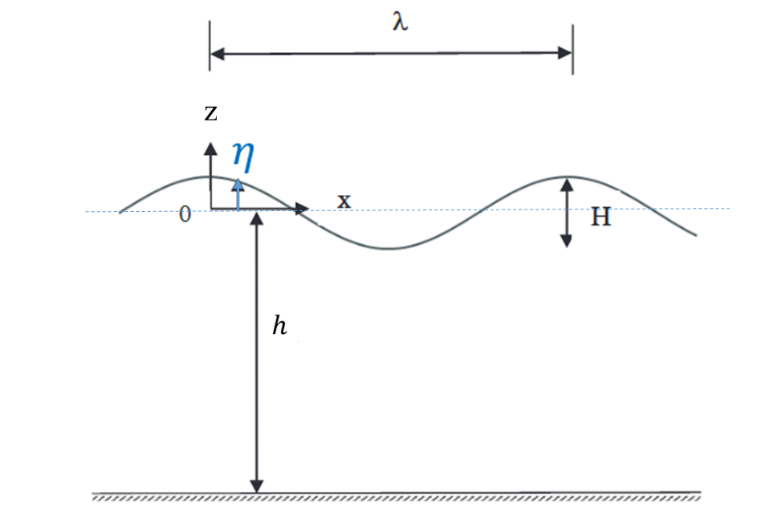
The free surface \(\mathrm{\eta }\) as a function of space \(x\) and time \(t\) is expressed:

(1.1)#\[ \ mathrm {\ eta} (x, t) =\ frac {H} {2}\ mathrm {cos} (kx-\ mathrm {\ omega} t)\]

with \(k=\frac{2\mathrm{\pi }}{\mathrm{\lambda }}\) the wave number and \(\mathrm{\omega }=\frac{2\mathrm{\pi }}{T}\) the pulsation.

The speed of fluid \({V}_{w}=(u,v,w)\) is as follows:

(1.2)#\[\begin{split} \ begin {array} {c} u (x, z, t) =0\\ v (x, z, t) =\ frac {H} {2}\ mathrm {\ omega}\ frac {\ mathrm {sinh} (k, z, t) =0\\ v (x, z, t) =\ frac {array} {c}}\ mathrm {sinh} (\ mathrm {.} x-\ mathrm {\ omega} t)\\ w (x, z, t) =\ frac {H} {2}\ mathrm {\ omega}\ frac {\ mathrm {sinh} (k)} (k (h+z))} {\ mathrm {sinh} (kh)}\ mathrm {sin} (k\ mathrm {sinh})} {\ mathrm {sinh} (kh)}\ mathrm {sin} (k\ mathrm {sinh}} (k\ mathrm {sinh})} {\ mathrm {sinh} (kh)}\ mathrm {sin} (k\ mathrm {sinh})} {\ mathrm {sinh} (kh)}} x-\ mathrm {\ omega} t)\ end {array}\end{split}\]

The acceleration of the fluid is noted \({a}_{w}=\frac{\partial {v}_{w}}{\partial t}\).

1.4. Loads#

The cable is subject to drag forces induced by a field of regular waves of height \(H=3m\) and period \(T=12s\).

Note that Archimedes” weight and thrust are not taken into account in this problem.

Modeling A

The cable is subject to Morison’s efforts (drag term only):

(1.3)#\[ {F} _ {\ text {mor}} =\ frac {1} {2} {2} {2} {C} _ {d} {\ mathrm {\ rho}}} _ {w} _ {w} ({v} _ {w}} ^ {v} _ {w} ^ {v}} ^ {\ text {ortho}}}) ({v} _ {w}} ^ {v} _ {w} ^ {\ text {ortho}} - {v} _ {s} ^ {\ text {ortho}})\]

where \({v}_{w}\) and \({v}_{s}\) respectively designate the fluid speed and the solid speed (mechanical load input parameter FORCE_POUTRE). The symbol \(\text{ortho}\) represents the projection in the direction normal to the neutral fiber of the beam [1] _ . It should be noted that these are linear forces that are applied in a distributed manner on the beam.

Note: Morison’s efforts depend on the position of the beam; they should be mentioned as follower loadings in the calculations.