1. Reference problem

1.1. Device description

The system studied is represented by the rheological model below. It is composed of a non-linear element affected by the behavior DIS_ECRO_TRAC (between the nodes N1 and N2), a mass assigned to the node N2, a linear element (between the nodes N2 and N3).

Figure 1.1-a: Device model.

The equations governing the behavior of the nonlinear element are in [R5.03.17].

1.2. Modelizations

The models tested are on elements DIS_T, mesh SEG2. The characteristics of the discrete elements are of the type: K_T_D_L.

Note: The units of the parameters must agree with the unit of effort, the unit of lengths [R5.03.17]. For all models the units are homogeneous to [N], [mm].

Note: Models A and B treat the same system, with the same boundary conditions, the same load.

1.2.1. Modeling A

This modeling makes it possible to test the nonlinear behavior of the isotropic work hardening type, in the local discrete x-direction, of the DIS_ECRO_TRAC law with the DYNA_NON_LINE operator.

1.2.2. B modeling

This modeling makes it possible to test the nonlinear behavior of the isotropic work hardening type, in the local discrete x-direction, of the DIS_ECRO_TRAC law with the DYNA_VIBRA operator.

1.2.3. C modeling

This modeling makes it possible to test the nonlinear behavior of the isotropic work hardening type, in the local tangent plane of the discrete, of the DIS_ECRO_TRAC law with the DYNA_NON_LINE operator.

1.2.4. D modeling

This modeling makes it possible to test the nonlinear behavior of the isotropic work hardening type, in the local tangent plane of the discrete, of the DIS_ECRO_TRAC law with the DYNA_VIBRA operator.

1.2.5. E modeling

This modeling makes it possible to test the nonlinear behavior, such as kinematic work hardening, in the local tangential plane of the discrete, of the DIS_ECRO_TRAC law with the DYNA_NON_LINE operator.

1.2.6. F modeling

This modeling makes it possible to test the nonlinear behavior, such as kinematic work hardening, in the local tangential plane of the discrete, of the DIS_ECRO_TRAC law with the DYNA_VIBRA operator.

1.3. Material properties

1.3.1. A and B models

The stiffness of the linear device is \({k}_{\mathit{lin}}\phantom{\rule{2em}{0ex}}=\phantom{\rule{2em}{0ex}}400N.\mathit{mm}\).

The mass is \(M\phantom{\rule{2em}{0ex}}=\phantom{\rule{2em}{0ex}}200\mathit{kg}\).

The non-linear behavior used in the test case is shown in the figure:

• Elastic behavior up to point \((\mathrm{0.5mm},\mathrm{200.0N})\).

• Nonlinear behavior, governed by the following equation:

\[\]

: label: EQ-None

R (p) =frac {{K} _ {mathit {elas}} .p} {left [1+ {left (frac {{k} _ {mathit {elas}} .p} .p} {{F} _ {u} _ {u}} — {F} _ {elas}}} .p} {{F} _ {elas}}} .p} {{F} _ {elas}} .p} {{F} _ {u}} — {F} _ {y}}right)} ^ {n}right]} ^ {(1/n)}} .p} {{F} _ {(1/n)}}

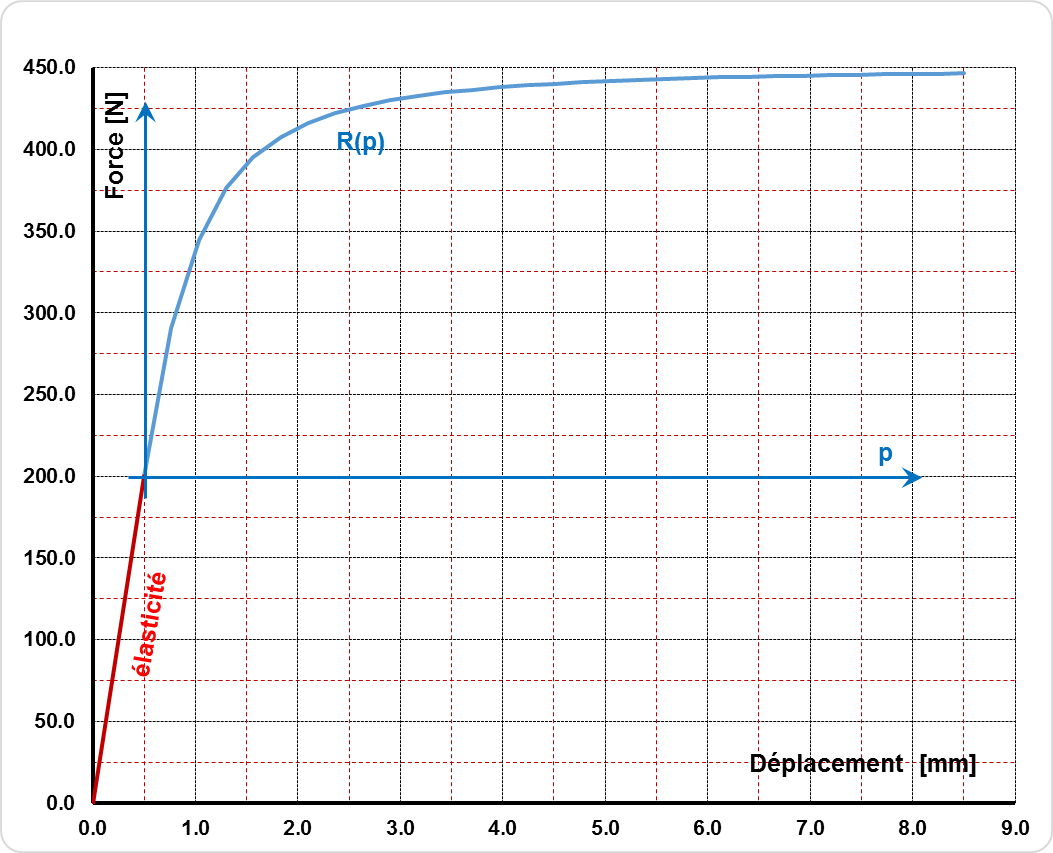
Figure 1.3.1-a : Nonlinear behavior

1.3.2. C and D modeling

The stiffness of the linear device is \({k}_{\mathit{lin}}=400\mathit{N.mm}\).

The mass is \(M=200\mathit{kg}\).

The behavior is of the « isotropic work hardening » type in the tangential plane local to the element. It is defined by the following function:

fctsy2 = DEFI_FONCTION (NOM_PARA = « DTAN »,

VALE = ( 0.0, 0.0, 0.0, 0.1, 0.1, 100.0, 0.2, 120.0, 20.2, 370.0),

)

1.3.3. SE and F modeling

The stiffness of the linear device is \({k}_{\mathit{lin}}=400\mathit{N.mm}\).

The mass is \(M=200\mathit{kg}\).

The behavior is of the « kinematic work hardening » type in the tangential plane local to the element. It is defined by the following function:

fctsy2 = DEFI_FONCTION (NOM_PARA = « DTAN »,

VALE = ( 0.0, 0.0, 0.0, 0.1, 100.0, 20.1, 350.0),

)

1.4. Boundary conditions and loads

1.4.1. A and B models

Nodes N1, N2, N3 are stuck in the Y and Z directions.

For models A and B, the nodes N1 and N3 are subject to displacement \(U(t)\) in the X direction.

For modeling B, nodes N1 and N3 are subject to displacement \(U(t)\), speed \(V(t)\), and acceleration \(\mathrm{\gamma }(t)\) in the X direction.

The condition while traveling as a function of time:

\(U(t)={U}_{0}.\mathrm{sin}(2\pi .\mathit{f.t})/(2\pi .f)\) with \(f=0.5\mathit{Hz}\) and \({U}_{0}=\mathrm{6.0mm}\)

The speed condition as a function of time: \(V(t)\phantom{\rule{2em}{0ex}}=\phantom{\rule{2em}{0ex}}\dot{U}(t)\)

The accelerating condition as a function of time: \(\mathrm{\gamma }(t)\phantom{\rule{2em}{0ex}}=\phantom{\rule{2em}{0ex}}\ddot{U}(t)\)

1.4.2. C, D, E, and F models

Nodes N1, N2, N3 are locked in the X direction.

For C, D, E, and F models, the nodes N1 and N3 are subject to \(U(t)\) displacement in the Y and Z directions.

For modeling B, the nodes N1 and N3 are subject to displacement \(U(t)\), speed \(V(t)\), and acceleration \(\gamma (t)\) in the Y and Z directions.

Travel conditions are functions of time:

\(\mathit{Depl}={U}_{1.}\mathrm{sin}(2\mathrm{\pi }.{f}_{1}.t)+{U}_{2.}\mathrm{sin}(2\mathrm{\pi }.{f}_{2}.t)+{U}_{3.}\mathrm{sin}(2\mathrm{\pi }.{f}_{3}.t)\)

Following the direction \(Y\): \((u,f)=[(\mathrm{0.20,0}.80),(\mathrm{0.15,1}.50),(\mathrm{0.10,3}.00)]\)

Following the direction \(Z\): \((u,f)=[(-\mathrm{0.20,0}.90),(\mathrm{0.15,2}.00),(-\mathrm{0.10,2}.80)]\)

The speed condition as a function of time: \(V(t)=\dot{U}(t)\)

The accelerating condition as a function of time: \(\gamma (t)=\ddot{U}(t)\)