1. Reference problem#

1.1. Geometry#

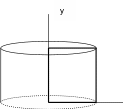
Figure 1.1-a: Problem Geometry

It is a cylinder with radius \(0.05m\) and height \(0.05m\).

The square in bold corresponds to the axisymmetric modeling used in [§3].

Material properties are described by the following parameters:

(Zirconium)

\(\rho {C}_{P}=2000000{\mathrm{J.m}}^{-3}\mathrm{.}°{C}^{-1}\)

\(\lambda =9999.9{\mathrm{W.m}}^{-1}\mathrm{.}°{C}^{-1}\)

Coefficient for metallurgy:

\(\mathrm{teqd}=809°C\), \(K=1.135E-2\), \(n=2.187\)

\(\mathrm{t1c}=831°C\), \(\mathrm{t2C}=0.\), \(\mathrm{qsr}=14614\), \(\mathrm{Ac}=1.58E-4\)

\(m=4.7\), \(\mathrm{t1r}=\mathrm{949,1}°C\), \(\mathrm{t2r}=0\), \(\mathrm{Ar}=-5.725\), \(\mathrm{Br}=0.05\)

The temperature is imposed on the entire cylinder at times \(t=\mathrm{0s},\mathrm{120s}\) and \(\mathrm{240s}\).

\(T(x,y,t=0)=20°C\)

\(T(x,y,t=120)=1200°C\)

\(T(x,y,t=240)=20°C\)

The following variables are initialized to the following values:

\(\mathrm{V1}(x,y,t=0)=1.0\)

\(\mathrm{V2}(x,y,t=0)=0.0\)

\(\mathrm{V3}(x,y,t=0)=0.0\)

\(\mathrm{V4}(x,y,t=0)=0.0\)

\(\mathrm{V1}\) : proportion of the cold phase \(\alpha\)

\(\mathrm{V2}\) : proportion of the cold phase \(\alpha\) , mixed with the phase \(\beta\)

\(\mathrm{V3}\) : node temperatures

\(\mathrm{V4}\) : time corresponding to the temperature at which the start or end of the equilibrium transformation