1. Reference problem#
1.1. Geometry#
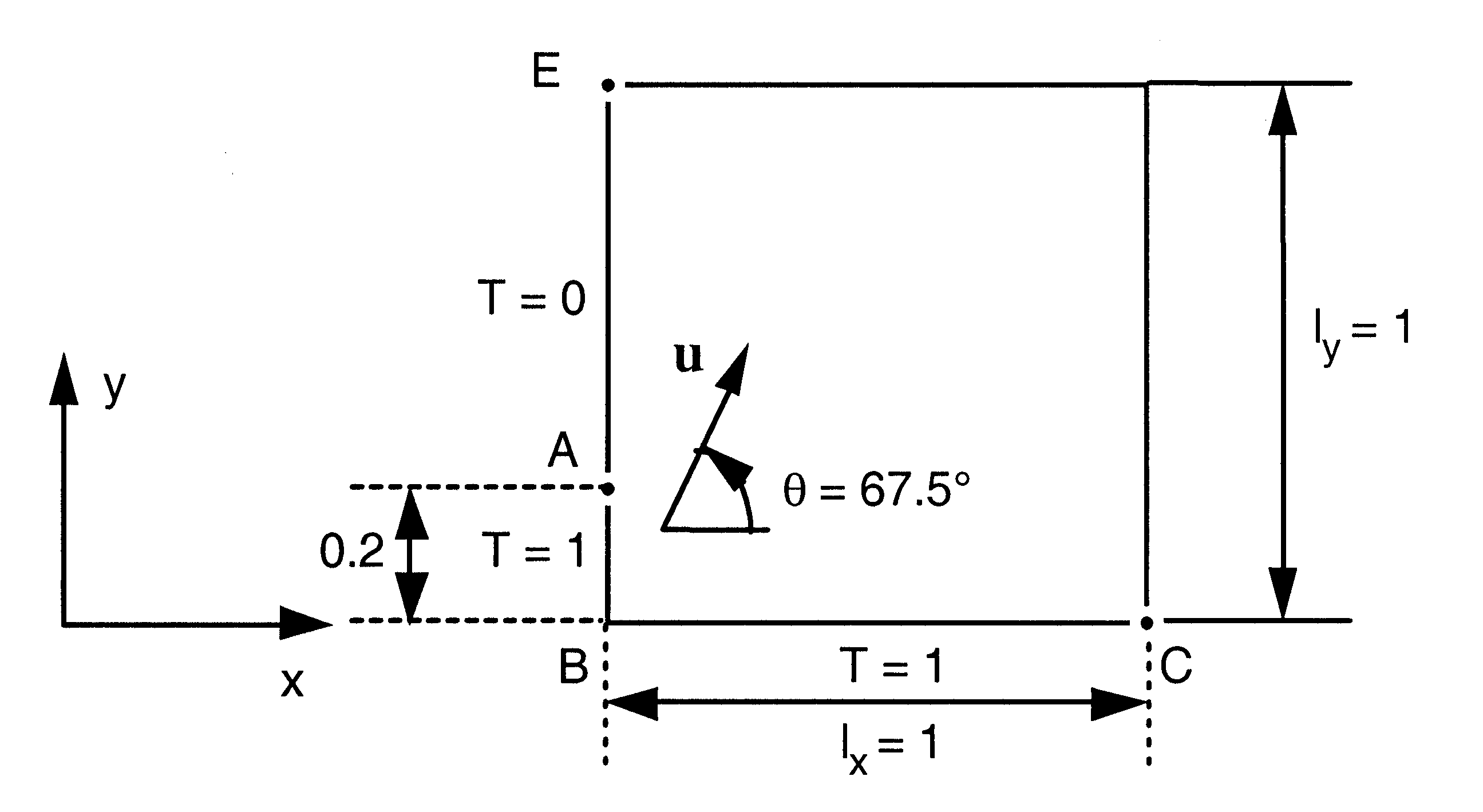
We consider the plane thermal problem of a square cavity (with a side equal to 1) where heat propagates:
by convection (i.e. the particles constituting the middle of the cavity move at a speed \(u\) assumed to be constant here); the speed \(u\) is supposed to make an angle of \(67.5°\) with the axis \(x\),
by conduction.
1.2. Material properties#
We take \(\rho {C}_{P}=1.\) \(\lambda ={10}^{-6}\)
Hence a diffusivity \(\alpha =\frac{\lambda }{\rho {C}_{P}}={10}^{-6}\)
and as we take \(\parallel u\parallel =1\), we have the Peclet number \({p}_{e}=\frac{\parallel u\parallel \mathrm{.}L}{\alpha }={10}^{6}\) (\(L\) is the characteristic length, here \(L=1.\)).
1.3. Boundary conditions and loads#
On segments \(\mathrm{AB}\) and \(\mathrm{BC}\), a temperature \(T=1.\) is imposed
On segment \(\mathrm{AE}\), we impose a temperature \(T=0.\)
On the other 2 sides, we have the condition by default, namely, we have zero flow.