1. Reference problem#
1.1. Geometry#
Consider a quarter of a 20 cm high pipe. The internal diameter is 4.118 cm and the external diameter is 4.746 cm (resulting in a thickness of 0.628 cm).
The geometry can be visualized in the figure, with the adjusted mesh that will be used.
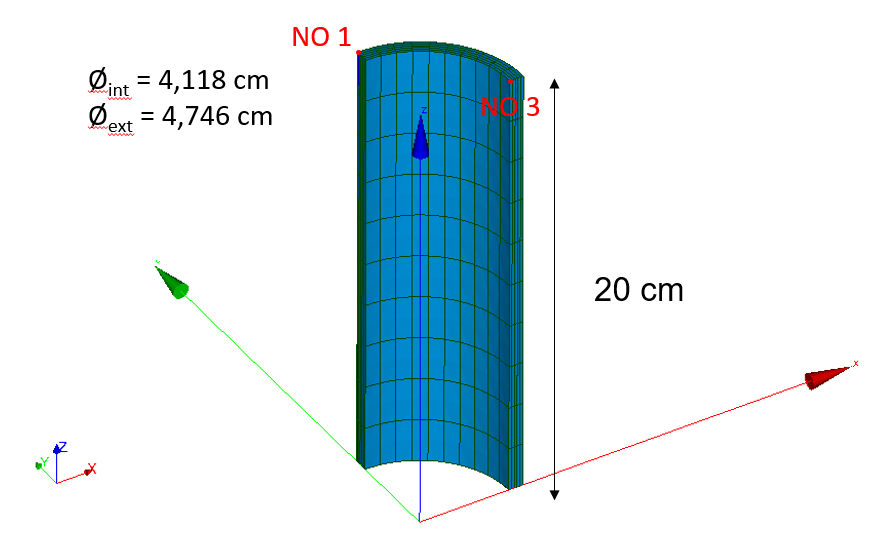
Figure 1.1-a : Geometry and mesh of a quarter pipe
1.2. Material properties#
The quarter pipe consists of an orthotropic material whose properties are as follows:
Young modules: \({E}_{L}=10\mathit{GPa}\), \({E}_{T}=10\mathit{GPa}\), and \({E}_{N}=50\mathit{GPa}\)
Poisson coefficients: \({\nu }_{\text{LT}}=\mathrm{0,1}\), \({\nu }_{\text{LN}}=\mathrm{0,06}\), and \({\nu }_{\text{TN}}=\mathrm{0,06}\)
shear modules: \({G}_{\text{LT}}=5\mathit{GPa}\), \({G}_{\text{LN}}=2\mathit{GPa}\) and \({G}_{\text{TN}}=2\mathit{GPa}\)
It is an isotropic transverse material whose isotropy axis is axis \(N\) (cylinder thickness axis).
1.3. Boundary conditions and loads#
The underside of the quarter pipe is embedded.
A distributed force of components \(\mathit{FX}=\mathrm{0,5}\mathit{MPa}\), \(\mathit{FY}=\mathrm{0,5}\mathit{MPa}\) and \(\mathit{FZ}=500\mathit{MPa}\) is applied to the upper face.