1. Reference problem

1.1. Geometry

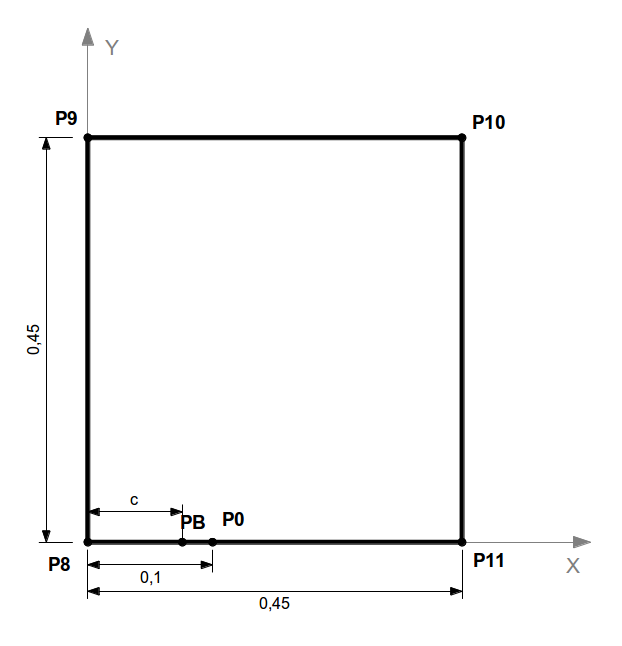
Figure 1.1 Problem geometry

1.2. Material properties

Young’s module	\(E=2\times {10}^{11}\mathit{Pa}\)
Poisson’s Ratio	\(\nu =0.3\)

1.3. Boundary conditions and loads

Point \(\mathit{PB}\) is for applying force \({F}_{Y}\).

The position of point \(\mathit{PB}\) is different depending on the models, and is managed by the parameter \(C\).

The distance \(a\) separating the points \(\mathit{P8}\) and \(\mathit{P0}\) is a constant parameter (\(a=\mathrm{0,1}\)).

In the various models, the \(c/a\) ratio is modified.

The lip of the crack is line \(\mathit{P8P0}\). So \(\mathit{P0}\) is the crack front.

For all models (A, B, C and D):

Imposed displacement:

Embedding on side \(\mathit{P8P9}\)	\(\mathit{DX}=0\)
Embedding on side \(\mathit{P0P11}\)	\(\mathit{DY}=0\)

Imposed loading:

\[\]

: label: EQ-None

textrm {Nodal force on the point} mathit {PB}

Only the position of point \(\mathit{PB}\), and the resulting mesh, are different between the models (the size of the radius of the mesh radiating at the bottom of the crack is different depending on the models).