1. Reference problem#
1.1. Geometry#
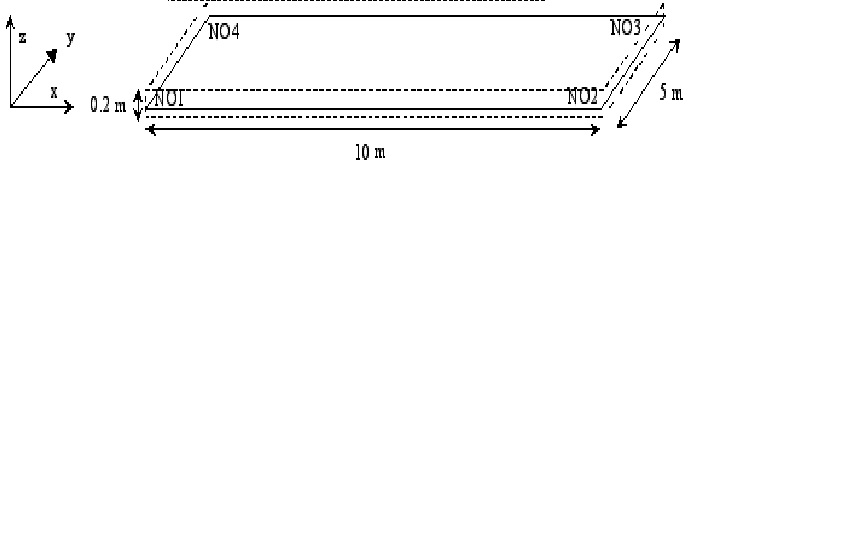
The aim is to model a reinforced concrete console of dimension \(10m\times 5m\times \mathrm{0,2}m\) with two layers of longitudinal reinforcements inserted into the concrete with \(>\) of coating.
1.2. Material properties#
Steels and concrete are supposed to be elastic.
Concrete console:
\(>\),
\(>\) to compare to shell modeling,
\(>\)
Thickness of the console: \(>\);
Steel frame sheets:
\(>\), \(>\), \(>\)
High reinforcement sheet: section per linear meter = \(\mathrm{0,2}{m}^{2}/\mathit{ml}\);
eccentricity = \(>\);
orientation: \(\mathit{Ox}\)
Low reinforcement sheet: section per linear meter = \(\mathrm{0,2}{m}^{2}/\mathit{ml}\);
eccentricity = \(>\);
orientation: \(\mathit{Ox}\)
1.3. Boundary conditions and loads#
Boundary conditions and loads break down as follows:
At first, between \(>\) and \(t=1\) the loads are as follows:
Edge \(NO1NO4\) \((B0X)\) embedded and edge \(NO2NO3\) \((B1X)\) stuck next \(\mathit{Oz}\).
Gravity
In a second step, between \(t=1\) and \(t=2\), we modify the condition on the edge to apply the following displacement \(\mathit{Oz}\):
\(DZ=-\mathrm{0,1}m\) on edge \(NO2NO3\) \((B1X)\) (flexure loading)