1. Reference problem#
1.1. Geometry#
A square plate, made of an orthotropic material inclined by 30 degrees with respect to the \(\mathrm{AB}\) edge.
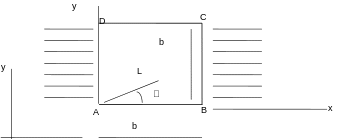
With \(b=1m\), any thickness (plane constraints), angle of orthotropy: \(\theta\) = 30 degrees.
1.2. Material properties#
The properties of the materials constituting the plate are:
orthotropic elastic:
\({E}_{L}=4.E10\mathrm{Pa}\)
\({E}_{T}=1.E10\mathrm{Pa}\)
\({G}_{LT}=0.45E10\mathrm{Pa}\)
\({G}_{\mathrm{TN}}=0.35E10\mathrm{Pa}\)
\({\mathit{NU}}_{LT}=0.3\)
Axis \(L\) is tilted by 30 degrees with respect to \(\mathrm{AB}\).
1.3. Boundary conditions and loads#
At point \(A\): \(\mathrm{DX}=0\), \(\mathrm{DY}=0\)
At point \(B\): \(\mathrm{DX}=0\),
Distributed line loading: \(\mathrm{Fx}={10}^{4}\mathrm{Pa}\) on \(\mathrm{BC}\)
Distributed line loading: \(\mathrm{Fx}=-{10}^{4}\mathrm{Pa}\) on \(\mathrm{DA}\)
1.4. Initial conditions#
Not applicable.