1. Reference problem#
1.1. Geometry#
We consider a cylindrical tube with a length \(2.17m\), an external diameter \(10\mathit{mm}\) and a thickness \(1\mathit{mm}\)
1.2. Material properties#
The material is isotropic elastic whose properties are:
\(E=210000\mathit{MPa}\)
\(\nu =0.3\)
\(\rho =7800\mathit{kg}/\mathit{m3}\)
1.3. Boundary conditions and loads#
The tube is supported by supports at several points according to the diagram below.
The mechanical characteristics of these supports are:
\(\mathit{Kx}=\mathit{Kz}=\frac{1.8{10}^{6}}{4}N/m\)
\(\mathit{Ky}=\frac{2.1{10}^{7}}{4}N/m\)
To break the axisymmetry of the model, which generates double modes, we add a point mass of \({10}^{-4}\mathit{kg}\), at a point on the lower support. At this point, the stiffness following x is also multiplied by 1.05. In addition, at another point on the lower support, the stiffness along z is multiplied by 0.95. On the one hand, this makes it possible to obtain a well-defined order of the modes according to the increasing frequency without disturbing the model too much, and on the other hand, to have static deformations that are not too collinear (linearly independent expansion base) for modeling a.
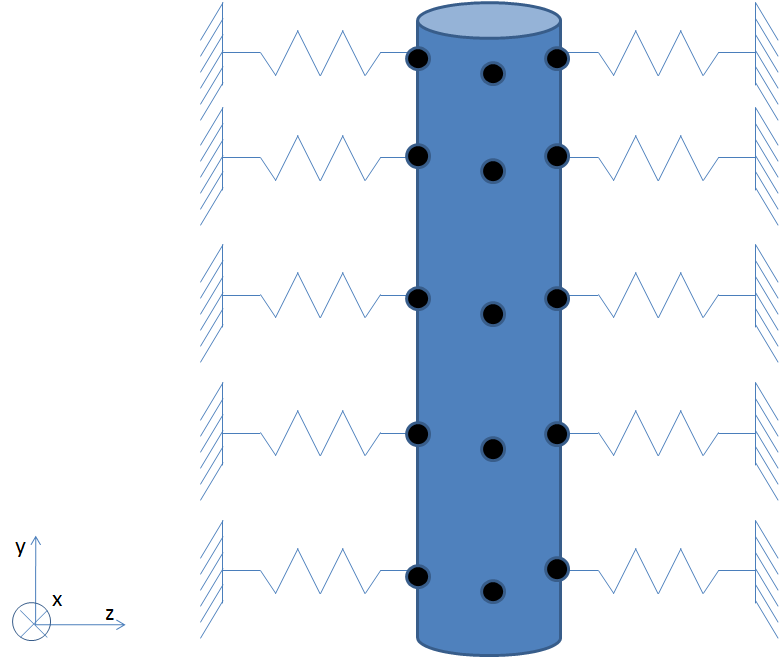
The dimensions of the support points are: 0.3 m, 0.8 m, 0.8 m, 1.29 m, 1.88 m and 2.09 m
To avoid overloading the illustration, the supports (springs) that are in the xOy plane are not shown.
Gauges were stuck inside the tube on two generators. Eight gauges were glued to each generator. The first generator is in the xOy plane and the second generator is in the yoZ plane.
The dimensions of the measurement points are: 0.2 m, 0.4 m, 0.63 m, 0.63 m, 0.63 m, 0.92 m, 1.22 m, 1.51 m, 1.80 m and 2.09m.
1.4. Initial conditions#
Néant