1. Introduction#
1.1. Geometry#
The study concerns a thick steel plate. Its geometry is simple. It is a simple flattened cube:
length \(\mathrm{2,0}\) meters, width \(\mathrm{2,0}\) meters and thickness \(\mathrm{0,03}\) meters [].
The plate is firmly embedded on one of its sides (ENCAS) and fixed on a vibrating table.
We want to calculate the displacement of a point located on the upper face in a corner of a plate, opposite to the embedment (point P) [].
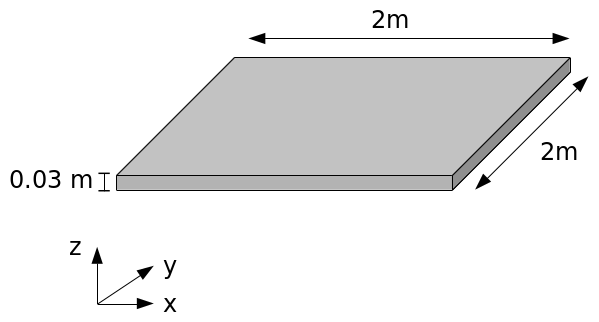
Figure 1.1-1

Figure 1.1-2
1.2. Materials#
For linear analyses, steel is considered to be an isotropic, linear elastic material:
Young’s modulus: \(E\mathrm{=}200000.{10}^{+6}\mathit{Pa}\),
Poisson’s ratio: \(\nu \mathrm{=}\mathrm{0,3}\),
density: \(\rho \mathrm{=}8000\mathit{kg}\mathrm{/}{m}^{3}\)
For non-linear analysis, this is a VMIS_ISOT_LINE behavior with \(\text{D\_SIGM\_EPSI}=2\mathit{GPa}\) (Young’s modulus divided by 100) and an elastic limit \(\mathit{SY}=200\mathit{MPa}\).
1.3. Boundary conditions and loading#
The plate is embedded on one of its sides.
The input signal is a simple sine with frequency \(15\mathit{Hz}\).
The amplitude is \(\mathrm{30g}\) horizontally and \(\mathrm{30g}\) vertically downwards (\(g=10m/{s}^{2}\)).
The duration of the signal is \(0.5s\).