3. Modeling A#
3.1. Digital model#
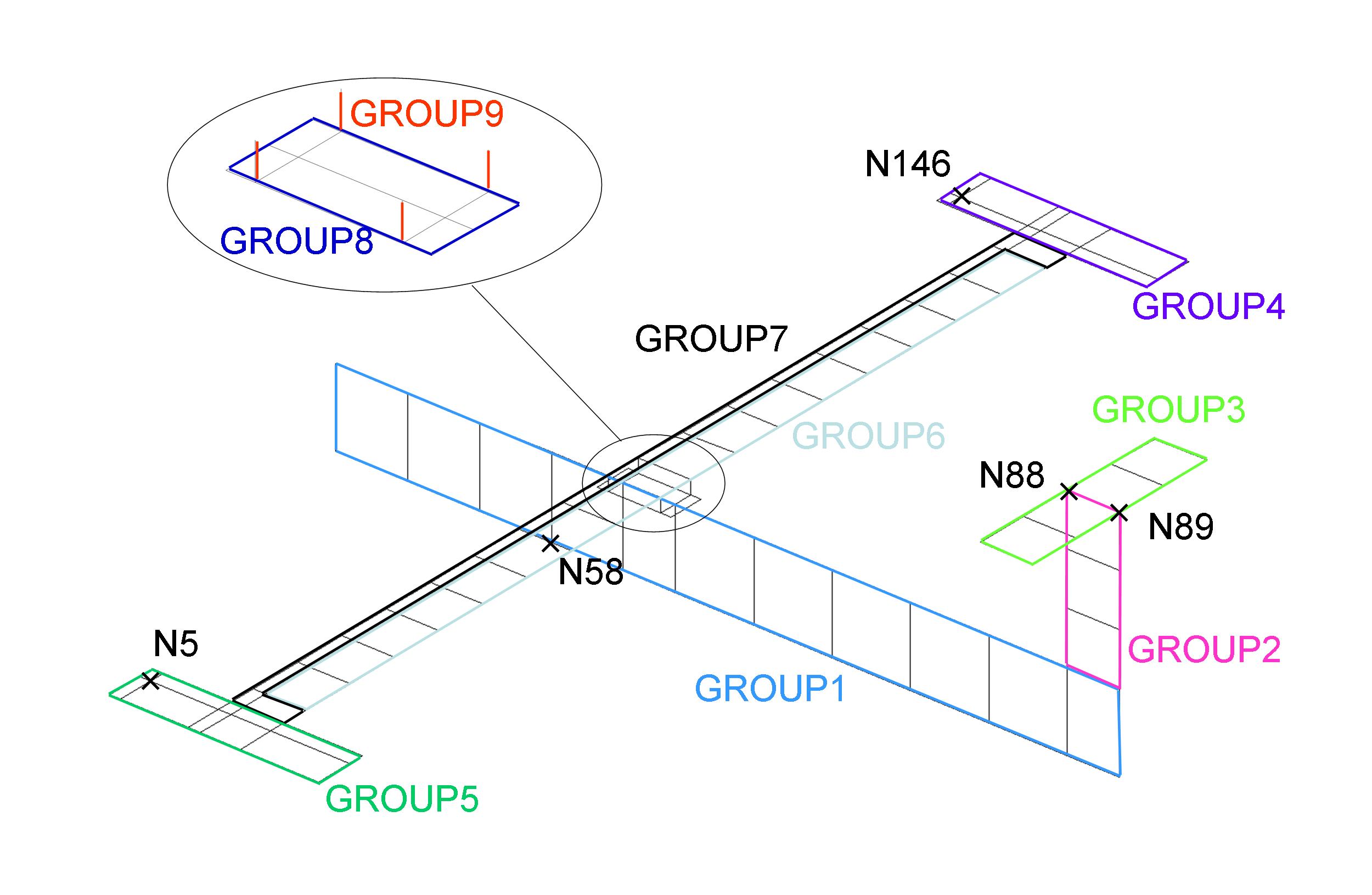
\(\mathrm{GROUP1}\) to \(\mathrm{GROUP8}\): Modeling DKT
\(\mathit{GROUP9}\): Modeling DIS_TR
formula \(\mathrm{GROUP10}:(\mathrm{N5},\mathrm{N88},\mathrm{N89},\mathrm{N146})\): Modeling DIS_T
Number of nodes |
\(138\) |
|||
Number of meshes |
\(86\) |
That is: |
||
SEG2 |
|
|||
QUAD4 |
|
3.2. Experimental model#
Modeling DIS_T: the characteristics of the experimental model have no physical reality, and the only objective is to be able to assign numbering and matrices that allow post-processing of the results. Thus, to read an experimental result (LIRE_RESU), you must first have defined mass and stiffness matrices, and to calculate MAC between two experimental mode bases, you must first have defined a NUME_DDL.
3.3. Expansion settings#
Expansion base: dynamic modes calculated on the dynamic model,
21 modes are calculated in band \(\mathrm{[}0.0,280.0\mathrm{]}\),
3.4. Tested sizes and results#
Digital mode matrix: it must be perfectly orthogonal in the sense of MAC. The sum of its components must therefore be equal to 5 (number of modes contained in structure MODESY).
Component |
Reference |
Tolerance |
|
Matrix obtained by MAC_MODES |
|
formula \(5.0\) |
|
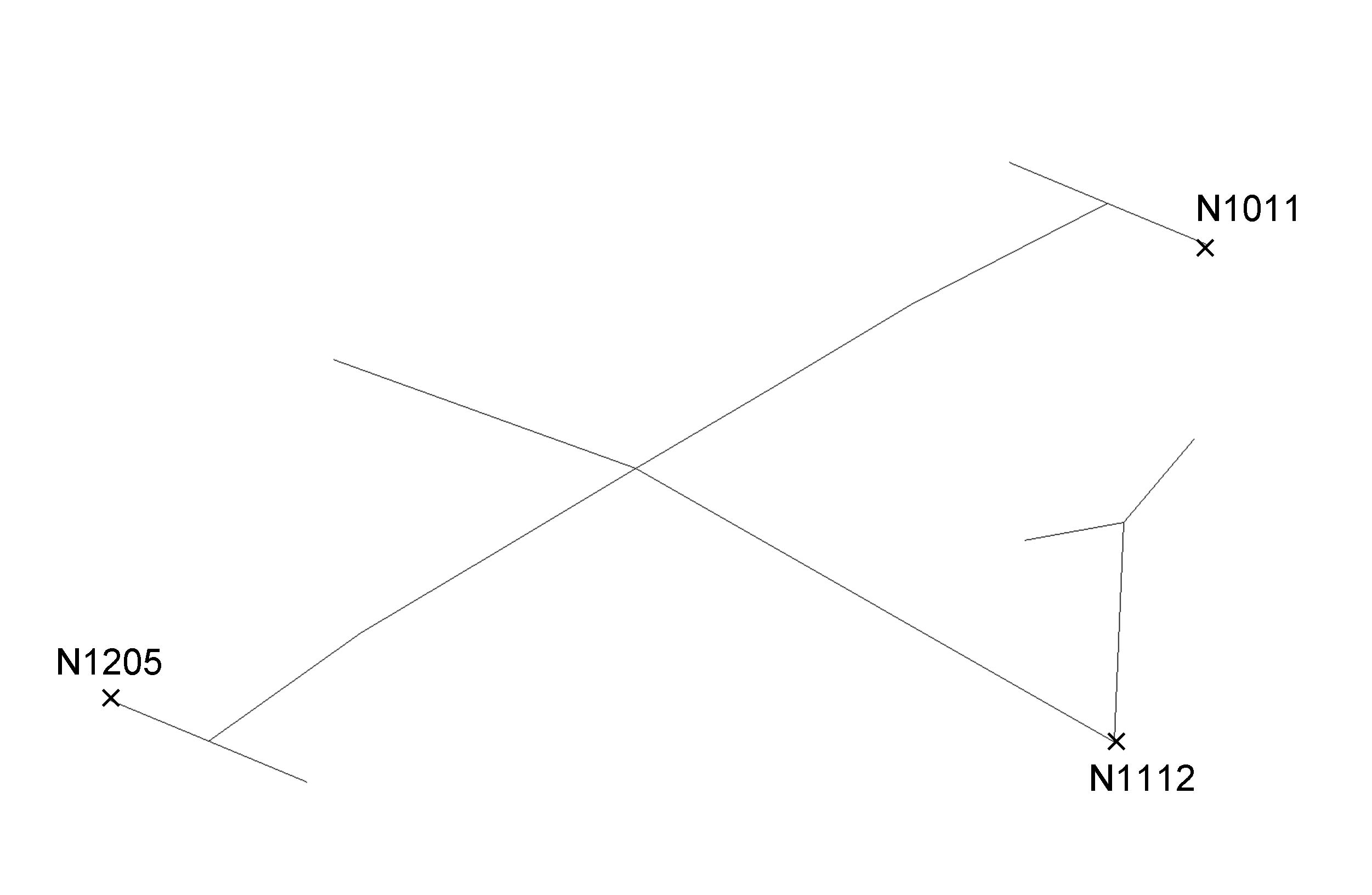
We check that the difference between FRF measured and extended/reprojected is relatively close to zero.
Bow |
Component |
Reference \((m\mathrm{/}{s}^{\mathrm{-}2})\) |
Tolerance |
|
Relative difference in acceleration |
\(\mathit{N1011}\) |
\(\mathit{D3}\) |
\(0.0\) |
\({10}^{\mathrm{-}2}\) |
\(\mathit{N1112}\) |
\(\mathit{D3}\) |
\(0.0\) |
\({10}^{\mathrm{-}2}\) |
|
\(\mathit{N1205}\) |
\(\mathit{D2}\) |
\(0.0\) |
\({10}^{\mathrm{-}2}\) |
We check that the auto MAC of the extended modes is close to the identity matrix, the extended modes having to be orthogonal. The result should be relatively correct (tolerance of \({10}^{\mathrm{-}2}\)). Note: for B modeling, this test is not performed, because in this case, the extended modes do not check the orthogonality condition. The dynamic expansion base gives better results here
Component |
Reference |
Tolerance |
||
Matrix obtained by MAC_MODES |
|
|
|
We check that the MAC diagonal between extended modes and digital modes is close to 1.
For each of the terms of the diagonal (21 modes in all), the following test is carried out:
Component |
Reference |
Tolerance |
||
Matrix obtained by MAC_MODES |
|
|
|