1. Reference problem#
1.1. Geometry#
We consider a hollow pipe with an outer radius \(10\mathit{mm}\), a thickness \(5\mathit{mm}\) and a length \(2m\).
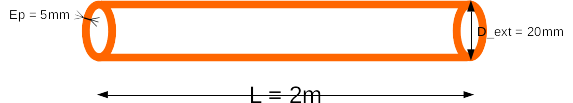
1.2. Material properties#
The material is isotropic elastic whose properties are:
\(E=210\mathit{GPa}\)
\(\nu =0.3\)
\(\mathrm{{\rm P}}=7800\mathit{kg}/{m}^{3}\)
\(\alpha =1.2E-5{K}^{-1}\)
Ramberg Osgood’s law used for post-treatments is written as:
\({ϵ}_{p}=K{(\frac{\sigma }{E})}^{1/n}\)
With:
\(K=0.01\)
\(n=2\)
In the case RCCM_RX =” OUI “, the values of the other parameters are as follows:
RP02_MIN = 128E6
RM_MIN = 410E6,
RP02_MOY = 163E6,
COEF = 1.
In cases where the parameters are given as a function, two different formulas are given on the two cells and a temperature field is constructed in such a way that the same values of the material parameters are found for each cell as in the constant cases.
1.3. Boundary conditions and loads#
A set of elastic calculations are performed independently on the beam-like structure.

1.3.1. Net weight#
A \(g=9.81m/{s}^{2}\) gravity field is imposed in the \(-Z\) direction. Point \(A\) is embedded.
1.3.2. Imposed displacement#
Point \(A\) is embedded. The structure is torsified at point \(B\) via an imposed angle \(\theta =0.02\mathit{rad}\) along the axis \(X\).
1.3.3. Thermal expansion#
Point \(A\) is embedded. Point \(B\) is stuck along the \(X\) axis. A variation in the temperature field \(\mathrm{\Delta }T=100°K\) generates compression in the beam.
1.3.4. Pressure imposed#
The pressure inside the pipe \(P=1\mathit{MPa}\) is taken into account.
1.3.5. Spectral seismic#
Point \(A\) is embedded. Point \(B\) is stuck along the \(Z\) axis. Spectral acceleration is imposed along the 3 axes \(X\), \(Y\) and \(Z\) with the respective ratios \(1.\), \(1.\) and \(0.5\):
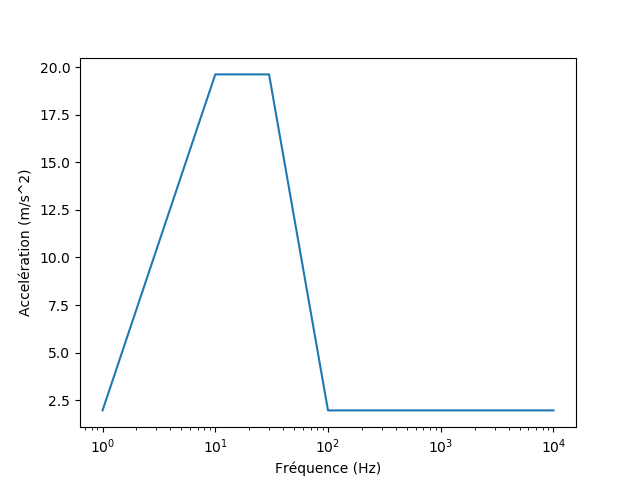
The first 4 dynamic natural modes and the static correction are taken into account via pseudo-modes along the 3 axes. Reduced amortization is set to \(2\text{\%}\).