1. Reference problem#

1.1. Geometry#

It is a 40 meter high beam, whose lower part (between altitudes 0 and 10 meters) is composed of stiff material while the upper part (above the 10-meter mark) is more flexible; the whole is equipped with a spring at the lower end (Table 1.1-1).

S

R O

Table 1.1-1 : Simplified Template

Point coordinates:

Knots	\(X\) (\(m\))	\(Y\) (\(m\))	\(Z\) (\(m\))
\(O\)			-1.
\(R\)
\(S\)
\(H\)

Table 1.1-2 : Node coordinates

Characteristics of the sections:

	Outer radius \({R}_{\mathit{ext}}\) (\(m\))	Thickness \({E}_{p}\) (\(m\))	GROUP_MA
write off			RADIER
built			BATI

Table 1.1-3 : Section characteristics

1.2. Material properties#

	Poisson’s ratio	Young’s modulus
\(({N\text{.}m}^{-2})\)) »	Density \(({\mathit{kg}\text{.}m}^{-3})\)	GROUP_MA
write off	0.2	\(3.5\text{ }E+10\)	\(2.5\text{ }E+03\)	RADIER
frame	0.2	\(3.5\text{ }E+08\)		\(2.5\text{ }E+03\)	BATI

Table 1.2-1

	Stiffness in x \(({N\text{.}\mathit{kg}}^{-1})\)	Y-stiffness \(({N\text{.}\mathit{kg}}^{-1})\))	Stiffness in z \(({N\text{.}\mathit{kg}}^{-1})\))	Mass \((\mathit{kg})\)	GROUP_MA
soil	\(1\text{.}\text{ }E+13\)	\(1\text{.}\text{ }E+13\)		\(1\text{.}\text{ }E+13\)		SOL

Table 1.2-2 : Material Properties

1.3. Boundary conditions and loads#

Boundary conditions:

Knot \(O\): \(DX=DZ=0\)

Knot \(R\): \(DRY=0\)

All knots: \(DY=DRX=DRZ=0\)

Single-support seismic loads, identical in all 3 directions:

Reduced depreciation taken into account: 0.07

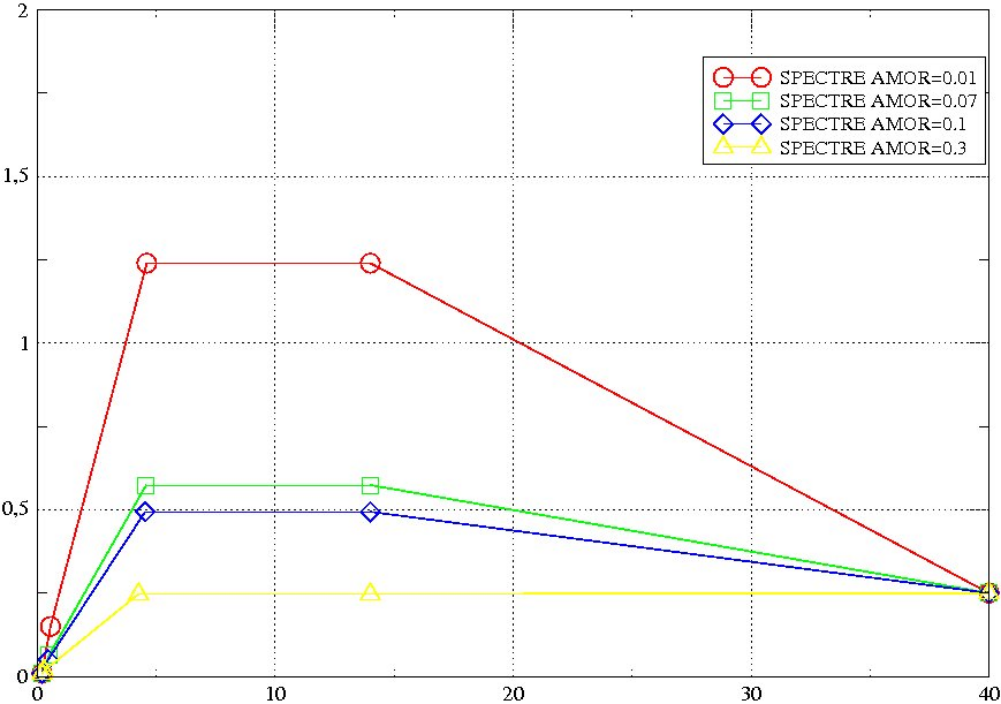
Fig. 1.3-1: Elastic response spectrum

abscissa: frequency ( \(\mathit{Hz}\) )/ordinate: acceleration ( \(g\) )