1. Reference problem#
1.1. Geometry#
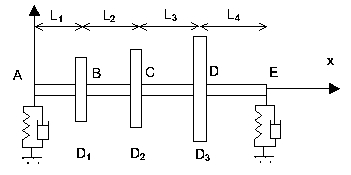
Modeling:
Mass (\(\mathrm{kg}\)) |
\({I}_{\mathrm{xx}}\) (\({\mathrm{kg.m}}^{2}\)) |
\({I}_{\mathrm{yy}}={I}_{\mathrm{zz}}\) (\({\mathrm{kg.m}}^{2}\)) |
|
Disc \({D}_{1}\) |
14.580130 |
0.1232021 |
0.6463858 |
Disk \({D}_{2}\) |
45.945793 |
0.97634809 |
0.4977460 |
Disc \({D}_{3}\) |
55.134951 |
1.1716177 |
0.6023493 |
Beam length:
\({L}_{1}=\mathrm{AB}=0.2m\)
\({L}_{2}=\mathrm{BC}=0.3m\)
\({L}_{3}=\mathrm{CD}=0.5m\)
\({L}_{4}=\mathrm{DE}=0.3m\)
Circular section:
Diameter: \(D=0.1m\)
1.2. Material properties#
\(E={2.10}^{11}\mathrm{Pa}\)
\(\nu =0.3\)
\(\rho =7800\mathrm{kg}/{m}^{3}\)
1.3. Boundary conditions and loads#
Elastic supports with viscous damping in \(A\) and \(E\)
\({K}_{\mathrm{yy}}={5.10}^{7}{\mathrm{N.m}}^{-1}\); \({K}_{\mathrm{zz}}={7.10}^{7}{\mathrm{N.m}}^{-1}\); \({K}_{\mathrm{yz}}={K}_{\mathrm{zy}}=\mathrm{0 }\)
\({C}_{\mathrm{yy}}={5.10}^{3}N/({\mathrm{m.s}}^{-1})\); \({C}_{\mathrm{zz}}={7.10}^{3}N/({\mathrm{m.s}}^{-1})\); \({C}_{\mathrm{yz}}={C}_{\mathrm{zy}}=0\)
Attention the amortizations have been multiplied by 10, compared to the harmonic calculation of test SHLL102 in order to obtain a faster attenuation of solid body modes in order to minimize the duration of the calculation. The other settings are the same.
Imbalance with value \(0.05\mathrm{m.kg}\), installed on node \(C\) (disk 2).