2. Benchmark solution

2.1. Calculation method used for the reference solution

The reference solution is analytical. In the absence of damping, it is a simple sine wave whose period is equal to the natural pulsation of the oscillator, \({\omega }_{0}=\sqrt{\frac{k}{m}}\), and whose amplitude is the initial elongation \(({x}_{0})\) of the spring. The \(x(t)\) position of the mass is given by the equation:

\(x(t)={x}_{0}\mathrm{cos}({\omega }_{0}t)\) (1)

So the speed of the mass is:

\(v(t)=-{\omega }_{0}{x}_{0}\mathrm{sin}({\omega }_{0}t)\) (2)

In the presence of viscous damping \(({c}_{[\mathrm{N.s}/m]})\), the oscillations become damped and position \(x(t)\) is written as:

\(x(t)={x}_{0}{e}^{-\zeta {\omega }_{0}t}[\mathrm{cos}(\omega t)+(\frac{\zeta }{\sqrt{1-{\zeta }^{2}}})\mathrm{sin}(\omega t)]\) (3)

where \(\zeta\) is the reduced depreciation given by \(\zeta =\frac{c}{2{\omega }_{0}m}\). \(\zeta\) is considered to be less than 1 to maintain oscillations. The pulsation is given by the formula \(\omega ={\omega }_{0}\sqrt{(1-{\zeta }^{2})}\). It is therefore different from the system’s natural pulsation \(({\omega }_{0})\).

2.2. Results

Case 1: conservative system (without amortization)

For this system, the natural pulsation \({\omega }_{0}=\pi \mathrm{rad}/s\). So the natural frequency is \({f}_{0}={\omega }_{0}/2\pi =\mathrm{0,5}\mathrm{Hz}\).

The displacement (in m) and the speed (in m/s) of the mass, given respectively by Eqs.1 and 2 are:

\(x(t)=\mathrm{cos}(\pi t)\) and \(v(t)=-\pi \mathrm{sin}(\pi t)\)

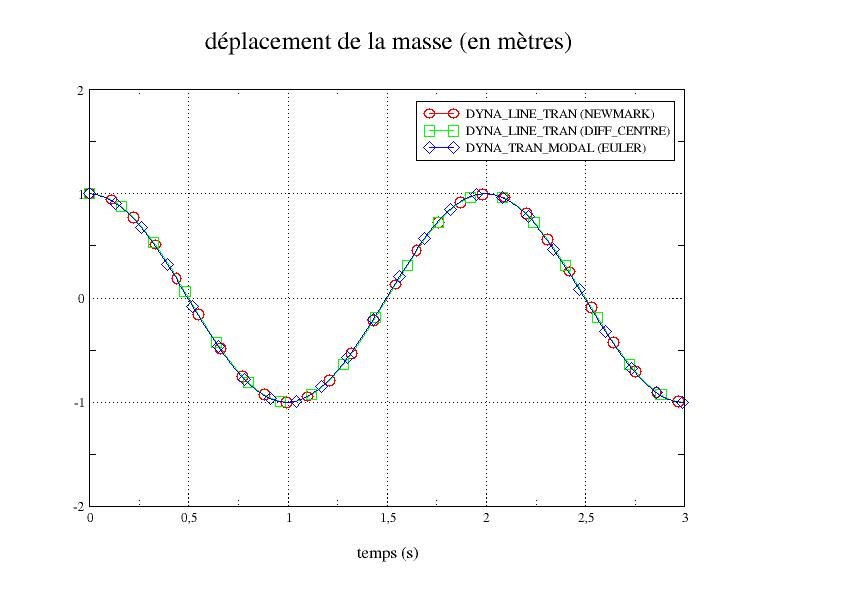
Case 2: viscous dissipative system

The reduced depreciation is \(\zeta =\mathrm{0,1}\). The pulsation is \(\omega =\mathrm{0,995}\pi \mathrm{rad}/s\) and the frequency is therefore \(f=\omega /2\pi =\mathrm{0,4975}\mathrm{Hz}\).

The displacement (in m) can then be calculated according to Eq.3.

2.3. Uncertainty about the solution

Analytical solution.