1. Reference problem#
1.1. Geometry#
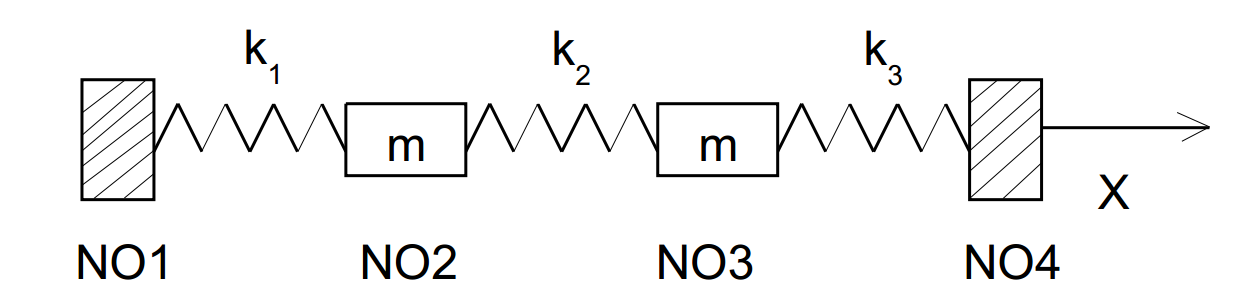
The structure is modelled by a set of 3 springs and 2 point masses.
1.2. Material properties#
Link stiffness: \({k}_{\mathrm{1 }}\mathrm{=}{k}_{\mathrm{2 }}\mathrm{=}k\mathrm{=}\mathrm{1000 }N\mathrm{/}m\); \({k}_{\mathrm{3 }}\mathrm{=}10k\mathrm{=}\mathrm{10000 }N\mathrm{/}m\)
point mass: \({m}_{\mathrm{2 }}\mathrm{=}{m}_{\mathrm{3 }}\mathrm{=}m\mathrm{=}\mathrm{10 }\mathit{kg}\).
1.3. Boundary conditions and loads#
boundary conditions
The only authorized movements are translations according to axis \(x\).
Points \(\mathit{NO1}\) and \(\mathit{NO4}\) are embedded: DX=DY=DZ= DRX = DRY = DRZ =0.
The other points are free to translate in the direction \(x\): DY=DZ= DRX = DRY = DRZ =0.
load
The structure is subject to multiple spectral seismic excitation and to differential displacements.
The pseudo-acceleration oscillator response spectra are simplified. Only the values corresponding to the 2 natural frequencies of the system are mentioned. They do not depend on depreciation:
at node \(\mathit{NO1}\):
\({\mathit{SRO}}_{\mathit{NO1}}({f}_{1})\mathrm{=}{A}_{11}\mathrm{=}7m\mathrm{/}{s}^{2}\)
\({\mathit{SRO}}_{\mathit{NO1}}({f}_{2})\mathrm{=}{A}_{21}\mathrm{=}5m\mathrm{/}{s}^{2}\)
\({\mathit{DDS}}_{\mathit{NO1}}\mathrm{=}D1\mathrm{=}\mathrm{-}0.04m\)
at node \(\mathit{NO4}\):
\({\mathit{SRO}}_{\mathit{NO4}}({f}_{1})\mathrm{=}{A}_{12}\mathrm{=}12m\mathrm{/}{s}^{2}\)
\({\mathit{SRO}}_{\mathit{NO4}}({f}_{2})\mathrm{=}{A}_{22}\mathrm{=}6m\mathrm{/}{s}^{2}\)
\({\mathit{DDS}}_{\mathit{NO4}}\mathrm{=}{D}_{2}\mathrm{=}0.06m\)
1.4. Initial conditions#
The system is initially at rest.