3. C modeling#
3.1. Characteristics of modeling#
Tested behavior: gursonTvergaardNeedlemanplasticflow_numericaljacobian.mfront
Elasto-plastic law with Gurson damage (model GTN in the literature).
Ref: « Analysis of the cup cone fracture in a round tensile bar ».
V.Tvergaard, A.Needleman, Acat Metallurgica 32 (1984) 157-169
the criterion is of the shape (f is the porosity)
\(F(\sigma ,f)={(\frac{{\sigma }_{\mathit{eq}}}{{\sigma }_{0}})}^{2}+2{q}_{1}f\mathrm{cosh}(\frac{3}{2}{q}_{2}\frac{{\sigma }_{h}}{{\sigma }_{0}})-1-{({q}_{1}f)}^{2}\le 0\)
Isotope work hardening is modified as follows (
\(R(p)=\mathit{R0}+{Q}_{1}(1–{e}^{-{b}_{1}p})+{Q}_{2}(1–{e}^{-{b}_{2}p})\)
Modeling: material point subject to imposed deformations:
\({\epsilon }_{\mathit{xx}}=\mathrm{0,02}t\), \({\epsilon }_{\mathit{yy}}=\mathrm{0,1}t\) \({\epsilon }_{\mathit{zz}}=0\)
Material properties:
Young |
200000 |
Fish |
0.3 |
R0 |
500 |
Q1 |
1e9 |
b1 |
1-e-6 |
Q2 |
0 |
b2 |
0 |
f0 |
1-e-3 |
fc |
1-e-2 |
delta |
2 |
beta |
0 |
Cp |
|
app |
1 e-5 |
q1 |
1.5 |
q2 |
1 |
3.2. Tested sizes and results#
Response curve \({\sigma }_{\mathit{yy}}=f({\epsilon }_{\mathit{yy}})\) is:
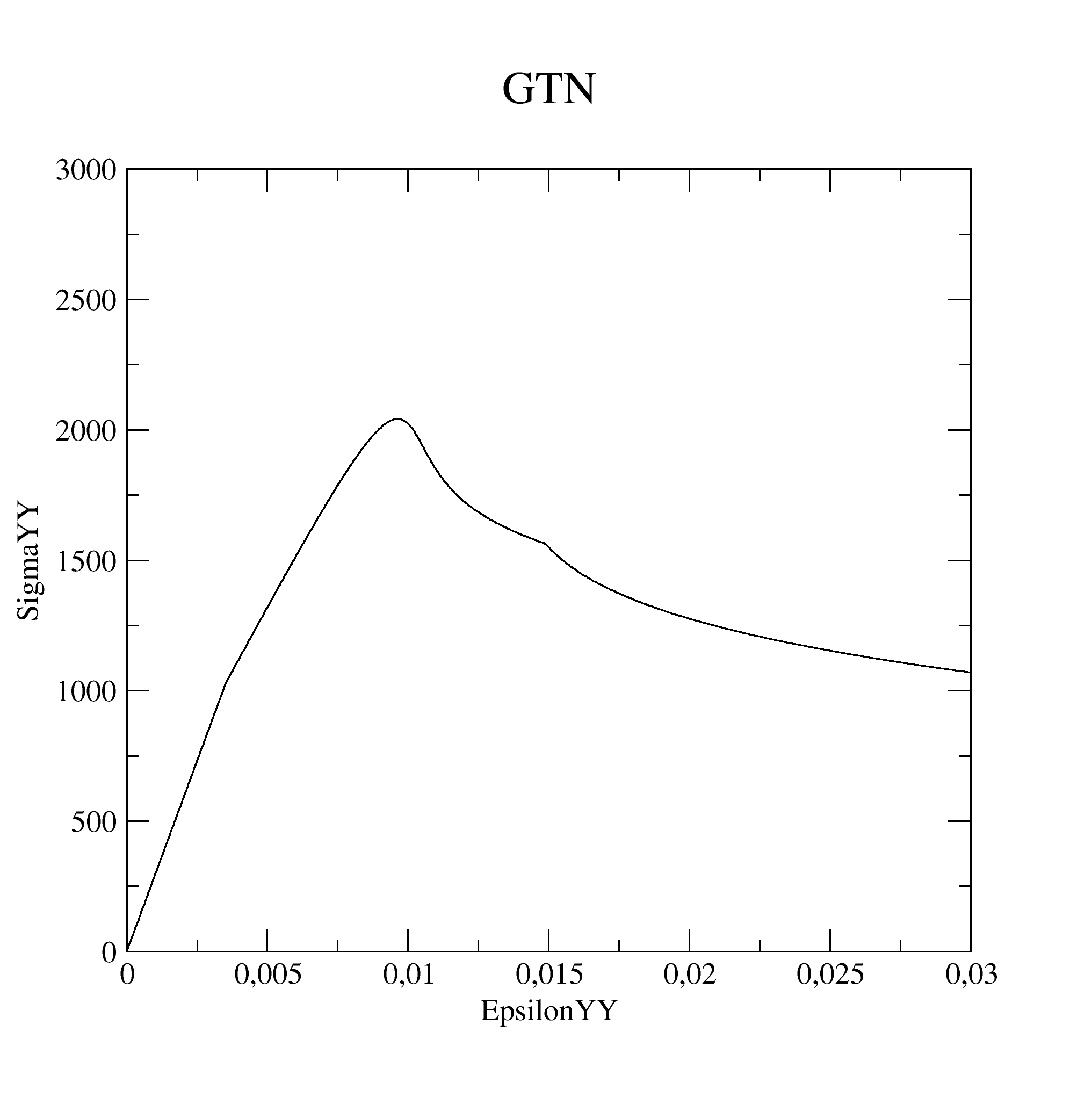
The tests are non-regression.
Identification |
Instants |
Reference |
Tolerance |
\({\sigma }_{\mathit{xx}}\) |
0.3 |
910.12 |
|
\({\sigma }_{\mathit{yy}}\) |
0.3 |
1069.37 |
|
\({\sigma }_{\mathit{zz}}\) |
0.3 |
870.308 |
|