1. Reference problem#
1.1. Geometry#
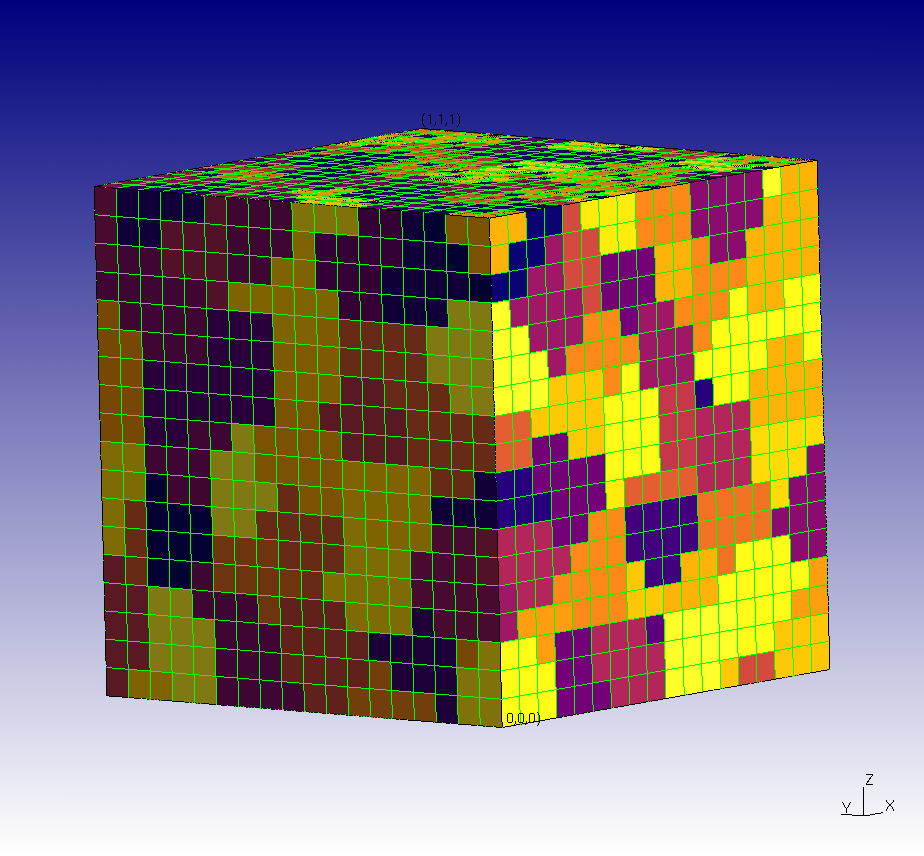
The aggregate is represented by a regulated hexahedral mesh occupying a volume with side 1.
It comprises 300 grains, defined by the belonging of each of the cells to a particular group of elements centered around a germ positioned randomly in the cube.
1.2. Material properties#
Elastic behavior with: |
Young’s module: |
Poisson’s ratio: |
|
Behavior mono-crystalline, with BCC24 sliding system.
The behavior of the single crystal is defined by:
Type of flow: MONO_VISC1 whose parameters are:
Isotropic work hardening type: MONO_ISOT1 ** whose parameters are:
(interaction between sliding systems)
No kinematic work hardening: MONO_CINE1
1.3. Boundary conditions and loads#
Face \(z\mathrm{=}0\) |
: |
Face \(y\mathrm{=}0\) |
: |
Face \(x\mathrm{=}0\) |
: |
Face \(z\mathrm{=}1\) |
: |
The load
is increasing linearly from 0 for \(t\mathrm{=}0\) to \(0.1\) for \(t\mathrm{=}\mathrm{100s}\).
To reduce the calculation time, this one is carried up to \(t\mathrm{=}\mathrm{1.8s}\), i.e. an imposed deformation of \(\text{0.18\%}\), in 3 increments.