1. Reference problem#

1.1. Geometry#

We consider a one-dimensional bar of length \(\mathrm{2L}=199\mathit{mm}\), at the center of which a discontinuity governed by cohesive behavior is arranged.

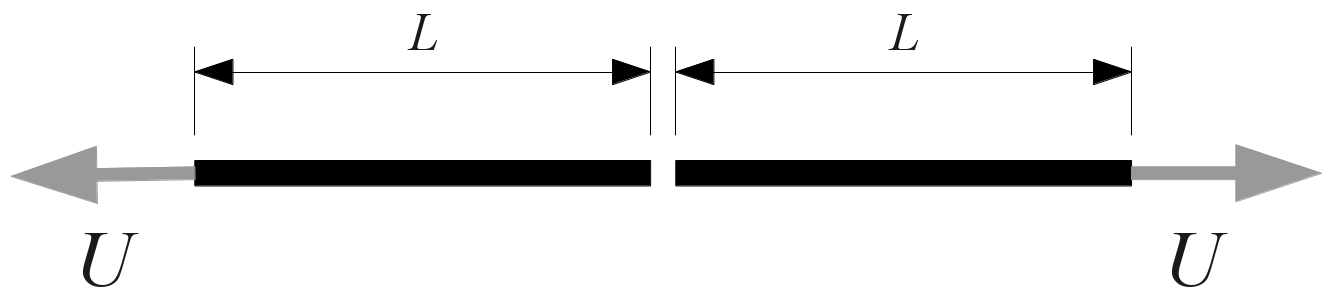
_images/100002010000053800000128C82A270D778CF653.png

Figure 1.1-a : One-dimensional bar under tension

We denote the space variable \(\widehat{x}\), and we mark the center of the bar by \(\widehat{x}=0\).

1.2. Material properties#

The behavior of the massif is linear elastic:

Young’s modulus: :math:`E=30000mathit{MPa}`

  • Poisson’s ratio: \(\nu =0\)

Cohesive behavior is described by an affine law in a softening regime (CZM_TAC_MIX for the interface elements used in modeling A, and CZM_LIN_REG for the joint elements used in modeling B), whose parameters are as follows:

  • Critical constraint: \({\sigma }_{c}=3\mathit{MPa}\)

  • Breakthrough energy: \({G}_{c}=0.1N/\mathit{mm}\)

The values for the additional numerical parameters are as follows:

  • \(\text{PENA\_LAGR}=45000\) for modeling A (CZM_TAC_MIX)

  • \(\text{PENA\_ADHERENCE}={10}^{-4}\) for B modeling (CZM_LIN_REG)

Note:

When only half of the bar is modelled (as is the case for modeling B) by imposing a symmetry condition, the value of the rupture energy is divided by 2.

1.3. Boundary conditions and loads#

The problem is one dimensional. The bar is called upon in traction, by imposing the same displacement of intensity \(U\) at each of its ends.

We increase the imposed displacement according to a ramp ranging from \(U=0\) to \({U}_{\mathit{test}}=2L\frac{{\sigma }_{c}}{E}=0.0199\mathit{mm}\)