1. Reference problem#
1.1. Geometry#
We consider a unit element of dimension 2 (quadrangle) or 3 (cube) according to the modeling. The element thickness, when required, is \(\mathrm{1m}\).
1.2. Material properties#
The material is isotropic elastic, whose properties are:
\(E\mathrm{=}1000\mathit{MPa}\)
\(\nu \mathrm{=}0.2\)
For modeling E, the Poisson’s ratio is zero.
1.3. Boundary conditions and loads#
1.3.1. Modeling A#
The unit-dimensional cube is shown on the. The displacement of the various nodes is imposed in accordance with.
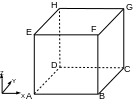
Figure 1.3.1-1: Modeling geometry A
knot |
\(\mathit{DX}\) |
|
|
|
\(A\) |
0.0 |
0.0 |
0.0 |
|
\(B\) |
1.0E-3 |
0.0 |
-6.0E-4 |
|
\(C\) |
2,0E-3 |
-2,0E-3 |
-3,0E-3 |
-3,0E-3 |
\(D\) |
1,0E-3 |
-2,0E-3 |
-2,4E-3 |
-2,4E-3 |
\(E\) |
0.0 |
2.2E-3 |
3.0E-3 |
3.0E-3 |
\(F\) |
1,0E-3 |
2,2E-3 |
2,4E-3 |
2,4E-3 |
\(G\) |
2,0E-3 |
2,0E-3 |
2,0E-4 |
0.0 |
\(H\) |
1.0E-3 |
2.0E-4 |
6.0E-4 |
6.0E-4 |
Table 1.3.1-1 : Moves of nodes s
1.3.2. B, C, and D models#
The geometry of the unit-dimensional quadrangle corresponds to face \(\mathit{ABCD}\) (). The displacement of the four nodes \(A\), \(B\), \(C\) and \(D\) is imposed in accordance with for the components \(X\) and \(Y\), the component \(Z\) being zero. When rotational degrees of freedom exist, they are stuck at point \(A\).
1.3.3. E modeling#
The geometry of the unit-dimensional quadrangle corresponds to face \(\mathit{ABCD}\) (). This is an axisymmetric model, whose axis is located \(\mathrm{1m}\) away from the \(\mathit{AD}\) edge. The movements of the nodes are zero, except for the \(Y\) component of the points \(C\) and \(D\), which is equal to \(\mathrm{1,0E-4}m\).
1.4. Initial conditions#
Néant