1. Reference problem#

1.1. Geometry#

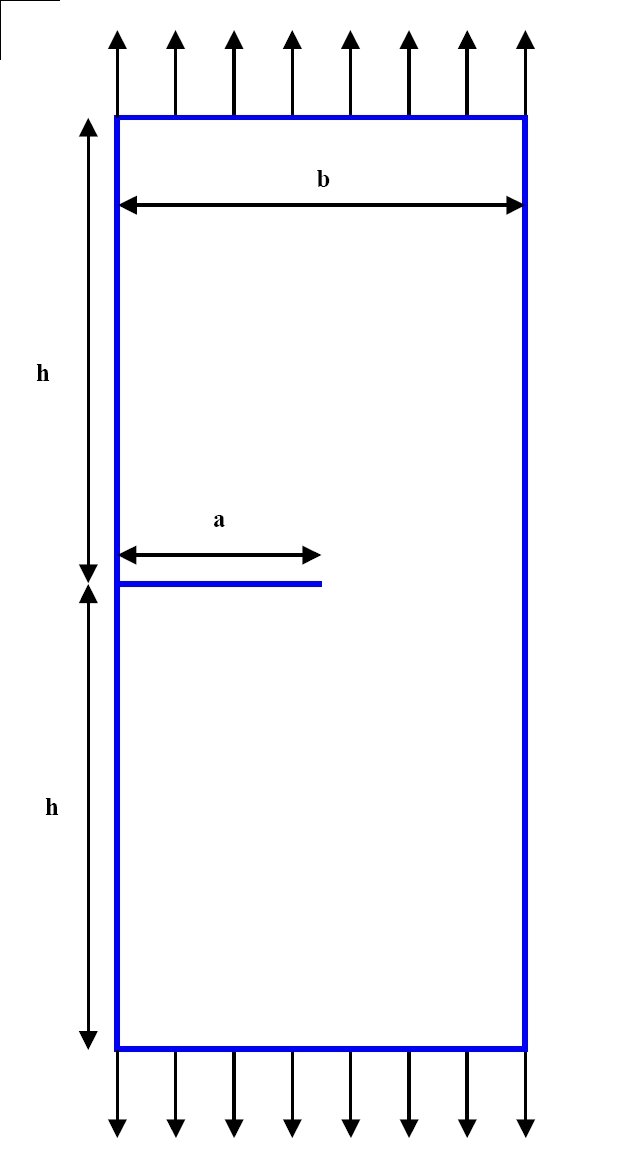
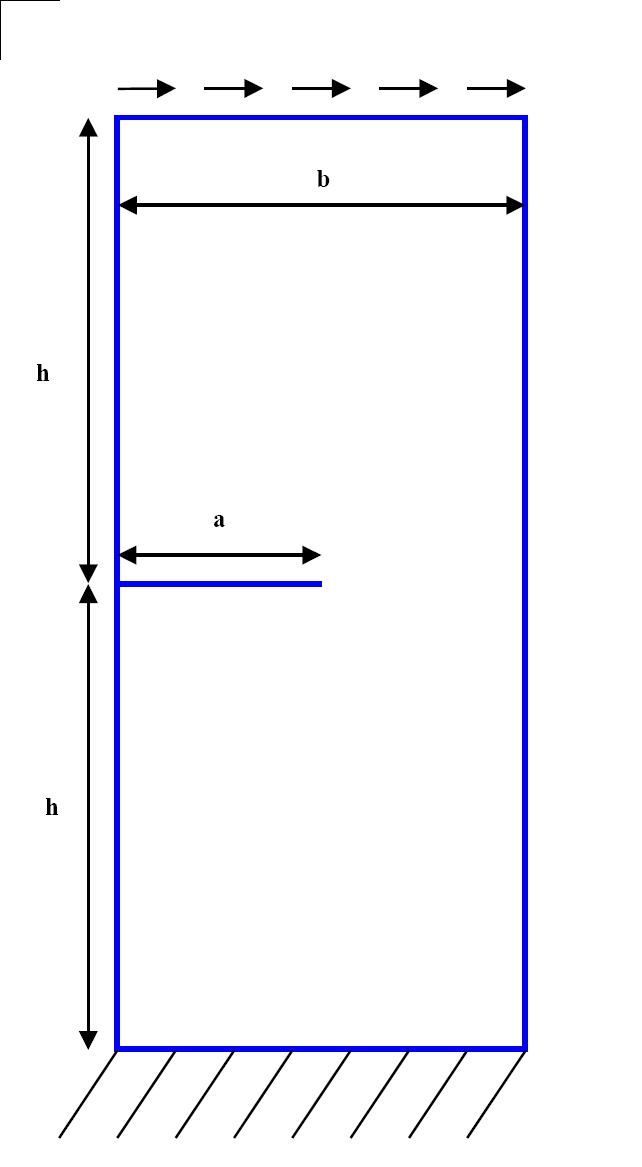
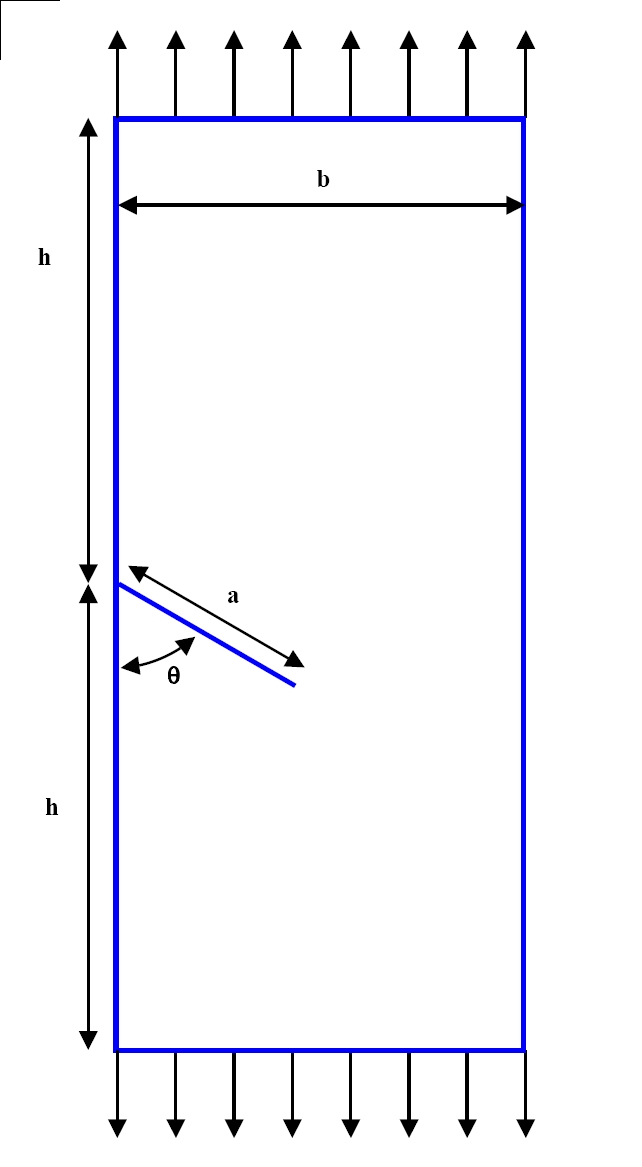
In this test, three configurations of cracked plates are considered. The first problem is a cracked plate subjected to a uniform tensile force (stress in \(I\) mode). The second problem is a cantilever beam subjected to a shear force (stress in mode \(I\) and in mode \(\mathrm{II}\)). Finally, the third problem is a plate with an inclined crack, subjected to a tensile force (stress in mode \(I\) and in mode \(\mathrm{II}\)).

The geometric parameters are as follows:

  • \(L/b=16/7\);

  • \(h=L/2\);

  • \(a/b=1/2\);

  • \(L=16\);

  • \(\theta =60\text{°}\).

_images/10000000000002820000048FE3BF93EBDCDDBD95.jpg _images/10000000000002820000048F04FFD806C637B4CA.jpg _images/10000000000002820000048F04A37600EE54B134.jpg

Table 1.1-1 :: ** Problem 1 (left), problem 2 (center), and problem 3 (right)

We define:

  • the \(\mathrm{HAUT}\) group of elements as the top edge;

  • mesh group \(\mathrm{BAS}\) as the bottom edge;

  • node group \(\mathrm{FONDFISS}\) (a single node) as the crack background;

  • node group \(\mathrm{BLOCAGE}\) (a single node) as the intersection of the crack extension and the right edge.

Moreover, to calculate the error in terms of quantity of interest, it is necessary to define another problem (the dual problem) which differs from the initial problem only by the Neuman conditions (the stiffness matrix and the Dirichlet conditions are the same). The specific loading of the dual problem in the context of the error estimation on stress intensity factors must be defined by means of functions to be imposed on the lips of the crack. To know how to define this load and how to impose it, we can refer on the one hand to the command files and on the other hand to the reference documentation on the estimation of error in quantity of interest [R4.10.06].

1.2. Material properties#

  • Young’s module: \(E=200000\text{MPa}\)

  • Poisson’s ratio: \(\nu =0.3\)

1.3. Boundary conditions and loads#

Problem 1:

    • Mesh group \(\mathrm{HAUT}\): \(\mathrm{FY}=1\)

    • Mesh group \(\mathrm{BAS}\): \(\mathrm{FY}=-1\)

    • Node \(\mathrm{FONDFISS}\): \(\mathrm{DY}=0\)

    • Node \(\mathrm{BLOCAGE}\): \(\mathrm{DX}=\mathrm{DY}=0\)

Problem 2:

    • Mesh group \(\mathrm{HAUT}\): \(\mathrm{FX}=1\)

    • Mesh group \(\mathrm{BAS}\): \(\mathrm{DX}=\mathrm{DY}=0\)

Problem 3:

    • Mesh group \(\mathrm{HAUT}\): \(\mathrm{FY}=1\)

    • Mesh group \(\mathrm{BAS}\): \(\mathrm{FY}=-1\)

    • Node \(\mathrm{FONDFISS}\): \(\mathrm{DY}=0\)

    • Node \(\mathrm{BLOCAGE}\): \(\mathrm{DX}=\mathrm{DY}=0\)