3. Operands#

The operands MODELE, CHAM_MATER, and CARA_ELEM are optional if RESULTAT is specified, mandatory if CHAM_GD is given.

3.1. Operand MODELE#

◊ MODELE = me,

The name of the model on which the option is calculated. The model name is optional as it is contained in the result data structure.

3.2. Operand CHAM_MATER#

◊ CHAM_MATER = to kill,

Material field associated with the mo model, optional because it is contained in the result data structure.

3.3. Operand CARA_ELEM#

◊ CARA_ELEM = character,

Carac elementary characteristics are necessary if structural elements (beam, plate, shell or discrete elements) exist in the model, which are optional because they are contained in the result data structure.

3.4. Operands NUME_COUCHE/NIVE_COUCHE#

◊ NUME_COUCHE = number,

In the case of a multilayer material, an integer value between 1 and the number of layers, necessary to specify the layer where it is desired to perform the elementary calculation. By convention, layer 1 is the lower layer (depending on the normal to the element) in the case of mechanical shell or thermal shell elements.

◊ NIVE_COUCHE =

For the nume layer defined by NUME_COUCHE, allows you to specify the ordinate where you want to perform the elementary calculation:

“INF “lower order of the diaper	(inner skin),
“SUP “upper layer ordinate	(outer skin),
“MOY “mean ordinate of the layer	(middle sheet by default).

3.5. Operand MODE_FOURIER#

◊ MODE_FOURIER =

Harmonic number for FOURIER: positive integer or zero (default = 0).

3.6. Operand GEOMETRIE#

♦ GEOMETRIE =/”INITIALE”, [DEFAUT]

/”DEFORMEE”,

Indicates whether we are working on the initial geometry or on the deformation. In the latter case, you must provide a travel field by CHAM_GD or RESULTAT.

3.7. Operands CHAM_GD/RESULTAT#

The options ENER_POT and ENER_CIN are calculated from a field at the nodes or by elements existing or extracted from a result.

3.7.1. Operand CHAM_GD#

♦/CHAM_GD = field,

Name of a field (for options ENER_POT and ENER_CIN).

For option ENER_POT, you need to provide a displacement field or a temperature field (see [§3.9]).

For option ENER_CIN, you must provide a speed field (without providing a frequency) or a displacement field and a frequency (see [§3.9]).

3.7.2. Operand RESULTAT#

/RESULTAT = resu,

Name of a result concept such as evol_elas, evol_ther, evol_ther, mode_meca, evol_noli, mult_elas, fourier_elas or dyna_trans.

Option ENER_POT:	evol_elas, evol_ther, mode_meca, mult_elas, fourier_elas evol_noliou dyna_trans.
Option ENER_CIN:	mode_meca, evol_elas, evol_ther, evol_noli, or dyna_trans.
ENER_ELAS and ENER_TOTALE options: \| evol_noli, evol_elas

Operands TOUT_ORDRE/NUME_ORDRE/NUME_MODE/LIST_ORDRE//NOEUD_CMP///FREQ/LIST_FREQ//INST/LIST_INST/purpose PRECISION CRITERE ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

See [U4.71.00].

3.8. Keyword MASS_INER#

3.8.1. But#

Keyword factor used to calculate mass, inertia, and center of gravity.

This option allows the following characteristics to be calculated on each element:

(\(\rho\) designating the density defined in DEFI_MATERIAU [U4.43.01] in [] by ELAS or ELAS_FO).

Mass: \(m=\underset{v}{\int }\rho \mathrm{dv}\)

Center of gravity: \({x}_{G}\mathrm{=}\frac{1}{m}\underset{v}{\mathrm{\int }}x\rho \mathit{dv};{y}_{G}\mathrm{=}\frac{1}{m}\underset{v}{\mathrm{\int }}y\rho \mathit{dv};{z}_{G}\mathrm{=}\frac{1}{m}\underset{v}{\mathrm{\int }}z\rho \mathit{dv}\)

Inertia tensor at the center of gravity \(G\) in the global coordinate system for describing the mesh:

\(\begin{array}{cc}{I}_{\mathit{xx}}(G)\mathrm{=}\underset{v}{\mathrm{\int }}({(y\mathrm{-}{y}_{G})}^{2}+{(z\mathrm{-}{z}_{G})}^{2})\rho \mathit{dv}& {I}_{\mathit{xy}}(G)\mathrm{=}\underset{v}{\mathrm{\int }}(x\mathrm{-}{x}_{G})(y\mathrm{-}{y}_{G})\rho \mathit{dv}\\ {I}_{\mathit{yy}}(G)\mathrm{=}\underset{v}{\mathrm{\int }}({(x\mathrm{-}{x}_{G})}^{2}+{(z\mathrm{-}{z}_{G})}^{2})\rho \mathit{dv}& {I}_{\mathit{xz}}(G)\mathrm{=}\underset{v}{\mathrm{\int }}(x\mathrm{-}{x}_{G})(z\mathrm{-}{z}_{G})\rho \mathit{dv}\\ {I}_{\mathit{zz}}(G)\mathrm{=}\underset{v}{\mathrm{\int }}({(x\mathrm{-}{x}_{G})}^{2}+{(y\mathrm{-}{y}_{G})}^{2})\rho \mathit{dv}& {I}_{\mathit{yz}}(G)\mathrm{=}\underset{v}{\mathrm{\int }}(y\mathrm{-}{y}_{G})(z\mathrm{-}{z}_{G})\rho \mathit{dv}\end{array}\)

Then calculate by « summation » the quantities relating to the overall structure.

The main inertia tensor consisting of the eigenvalues of the inertia matrix is calculated, as well as the 3 Euler angles associated with the main inertia coordinate system. These components are noted in the table:

IX_PRIN_G IY_PRIN_G IZ_PRIN_G ALPHA BETA GAMMA.

3.8.2. Syntax#

| MASS_INER =_F (

♦/TOUT = 'OUI',
/GROUP_MA = lgrma, [l_gr_mesh]
◊ ORIG_INER = (xp, yp [, zp]), [l_R]
),

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
◊ CARA_ELEM = carac, [cara_elem]
◊ | LAYER_NUMBER =
| LAYER_LEVEL =
◊ MODE_FOURIER =
◊ GEOMETRIE =
♦/CHAM_GD =
/RESULTAT =

Note

For the factor keyword MASS_INER, the template and material field are mandatory if RESULTATet CHAM_GDsont not present.

3.8.3. Operands#

♦ GEOMETRIE =/'INTIALE', [DEFAUT]
                    /'DEFORMEE',

Indicates whether we are working on the initial geometry or on the deformation. In the latter case, you must

provide a travel field by CHAM_GD or RESULTAT.

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

On a list of groups of elements. If there is more than one group of elements in the list, then a row is added to the output table which is the result on the union of the cells of the given groups in addition to the result per group. This new line corresponds to the group of elements” UNION_GROUP_MA “.

◊ ORIG_INER = (xp, yp [, zp]), [l_R]

Point in relation to which the inertia tensor will be calculated.

The inertia tensor at point \(P\) with coordinates (xp, yp, zp) is obtained from the inertia tensor at the center of gravity \(G\), the mass \(m\) of the structure and the coordinates of \(G\) by the formulas:

\(\begin{array}{}{I}_{\mathrm{xx}}(P)={I}_{\mathrm{xx}}(G)+m{x}_{\mathrm{PG}}^{2}\\ {I}_{\mathrm{yy}}(P)={I}_{\mathrm{yy}}(G)+m{y}_{\mathrm{PG}}^{2}\\ {I}_{\mathrm{zz}}(P)={I}_{\mathrm{zz}}(G)+m{z}_{\mathrm{PG}}^{2}\\ {I}_{\mathrm{xy}}(P)={I}_{\mathrm{xy}}(G)+m{x}_{\mathrm{PG}}{y}_{\mathrm{PG}}\\ {I}_{\mathrm{xz}}(P)={I}_{\mathrm{xz}}(G)+m{x}_{\mathrm{PG}}{z}_{\mathrm{PG}}\\ {I}_{\mathrm{yz}}(P)={I}_{\mathrm{yz}}(G)+m{y}_{\mathrm{PG}}{z}_{\mathrm{PG}}\end{array}\)

with

\(\begin{array}{}{x}_{\mathrm{PG}}={x}_{G}-{x}_{P}\\ {y}_{\mathrm{PG}}={y}_{G}-{y}_{P}\\ {z}_{\mathrm{PG}}={z}_{G}-{z}_{P}\end{array}\)

3.9. Keyword ENER_POT#

3.9.1. But#

Keyword factor used to calculate:

the potential deformation energy at equilibrium from displacements, in linear mechanics of continuous media (2D and 3D thermoelasticity):

\(\mathit{EPOT}\mathrm{=}\frac{1}{2}\underset{\mathit{élément}}{\mathrm{\int }}\varepsilon (\mathrm{U})\mathrm{\cdot }\mathrm{A}\varepsilon (\mathrm{U})\mathit{dv}\mathrm{-}\underset{\mathit{élément}}{\mathrm{\int }}\varepsilon (\mathrm{U})\mathrm{\cdot }\mathrm{A}{\varepsilon }^{\mathit{th}}(\mathrm{T})\mathit{dv}+\frac{1}{2}\underset{\mathit{élément}}{\mathrm{\int }}{\varepsilon }^{\mathit{th}}(\mathrm{T})\mathrm{\cdot }\mathrm{A}{\varepsilon }^{\mathit{th}}(\mathrm{T})\mathit{dv}\)

where \(A\) refers to the elasticity tensor,

the potential energy of deformation at equilibrium from displacements, in linear mechanics for structural elements:

\(\mathrm{EPOT}=\frac{1}{2}{U}^{T}{K}_{e}U-{U}^{T}{B}^{T}A{\varepsilon }^{\mathrm{th}}+\frac{1}{2}{\varepsilon }^{\mathrm{th}}A{\varepsilon }^{\mathrm{th}}\)

where \(K\) refers to the stiffness matrix

Note:

Strictly speaking, the potential energy of a structure is the opposite of these quantities.

the energy dissipated thermally at equilibrium in linear thermal from temperatures (cham_no_ TEMP_R):

\({W}_{\mathit{th}}\mathrm{=}\mathrm{-}\frac{1}{2}\underset{\Omega }{\mathrm{\int }}\mathrm{\nabla }T\mathrm{\cdot }\mathrm{K}\mathrm{\cdot }\mathrm{\nabla }Td\Omega\)

Note:

In the first two cases, you must give a displacement field behind the operand * RESULTATou CHAM_GD. In the latter case a temperature field.

Note:

In the case of calculating the option on a temperature field the dependence of the material parameters on temperature is taken into account via the control variables defined in AFFE_MATERIAU .

3.9.2. Syntax#

| ENER_POT =_F (

♦/TOUT = 'OUI',
     /GROUP_MA = lgrma, [l_gr_mesh]
)

Simple keywords: (see [§2])

◊ MODELE = mo, [model]

◊ CHAM_MATER = tamer, [chamber_master]

◊ CARA_ELEM = carac, [cara_elem]

◊ | LAYER_NUMBER =
     | LAYER_LEVEL =

◊ MODE_FOURIER =

♦/CHAM_GD =
     /RESULTAT =

Note

For the keyword factor ENER_POT, the model, the material field and possibly the structural element characteristics field are mandatory (unless RESULTATest provided) in order to determine the energy fields by elements beforehand.

3.9.3. Operands#

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

On a list of groups of elements.

3.9.4. Table produced#

The table contains, for each moment, the values of the energy and the percentage at the geometric location concerned:

INST	LIEU	ENTITE	TOTALE	POUR_CENT

5.50000E+00	MA	TOUT	4.00093E+12	1.00000E+02
5.50000E+00	GMA1	GROUP_MA	2.71323E+11	6.78151E+00

3.10. Keyword ENER_CIN#

3.10.1. But#

Keyword factor for calculating kinetic energy from a speed field or from a displacement field and a frequency.

If we gave a speed field, \({E}_{C}\mathrm{=}\frac{1}{2}{V}^{T}MV\).

If we gave a field of movement and a frequency, \({E}_{C}\mathrm{=}\frac{1}{2}{\omega }^{2}{U}^{T}MU\).

3.10.2. Syntax#

| ENER_CIN =_F (
    ◊ OPTION =/'MASS_MECA', [DEFAUT]
                                /'MASS_MECA_DIAG',
♦/TOUT = 'OUI',
  /GROUP_MA = lgrma, [l_gr_mesh]
)

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
◊ CARA_ELEM = carac, [cara_elem]
◊ | LAYER_NUMBER =
| LAYER_LEVEL =
◊ MODE_FOURIER =
♦/CHAM_GD =
/RESULTAT =

Note 1

For the keyword factor ENER_CIN, the model, the material field and possibly the structural element characteristics field are mandatory (unless RESULTATest provided) in order to determine the energy fields by elements beforehand.

Note 2

When you want to calculate the energy using the diagonal mass (to be consistent with the option you chose in the elementary calculation of mass matrices), you can specify “ MASS_MECA_DIAG “behind the keyword OPTION (not available in 2D). By default the full mass matrix is used.

3.10.3. Operands#

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

On a list of groups of elements.

3.10.4. Table produced#

The table contains, for each moment, the values of the energy and the percentage at the geometric location concerned:

INST	LIEU	ENTITE	TOTALE	POUR_CENT

5.50000E+00	MA	TOUT	4.00093E+12	1.00000E+02
5.50000E+00	GMA1	GROUP_MA	2.71323E+11	6.78151E+00

3.11. Keyword ENER_ELAS#

3.11.1. But#

Allows you to calculate the elastic deformation energy for each moment \(t\) after an elastic or elastoplastic calculation, on the topological selection chosen by the user.

The user can carry out this post-processing based on a result concept such as evol_noli or evol_elas. In the case of an evol_noli concept, the calculation performed depends on the choice of deformation made during the calculation.

In small deformations (DEFORMATION = PETIT or DEFORMATION = PETIT_REAC), the calculation is performed from the Cauchy stress field SIEF_ELGA by the Hooke expression:

\({E}^{e}(t)=\frac{1}{2}{\int }_{v}^{t}\sigma (t){D}^{-1}\sigma (t)\mathit{dv}\)

where \(D\) represents the elasticity operator.

in large multiplicative deformations (DEFORMATION = SIMO_MIEHE), the calculation is carried out using the Jacobian \(J\) of the transformation gradient and the specific measure of elastic deformation \({\overline{\mathrm{b}}}^{\mathrm{e}}\) of SIMO_MIEHE (see R5.03.21):

\({E}^{e}(t)={\int }_{v}^{t}\left[\frac{1}{2}\frac{E}{3\left(1-2\nu \right)}\left(\frac{1}{2}\left({J}^{2}(t)-1\right)-\mathrm{ln}J(t)\right)+\frac{1}{2}\mu \left(\mathit{tr}{\overline{\mathrm{b}}}^{\mathrm{e}}(t)-3\right)\right]\mathit{dv}\)

In the presence of thermal, a specific correction is carried out in order to best erase its effects on the Jacobian. This specific correction is detailed in R5.03.21.

in large logarithmic deformations (DEFORMATION = GDEF_LOG), the calculation is performed using the specific stress field \(T\) (see R5.03.24) by the expression:

\({E}^{e}(t)=\frac{1}{2}{\int }_{v}^{t}T(t){D}^{-1}T(t)\mathit{dv}\)

3.11.2. Syntax#

| ENER_ELAS=_F (
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgrma, [l_gr_mesh]
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
◊ CARA_ELEM = carac, [cara_elem]
◊ | LAYER_NUMBER =
| LAYER_LEVEL =
◊ MODE_FOURIER =
♦ RESULTAT =

3.11.3. Operands#

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

3.11.4. Table produced#

The table contains, for each moment, the values of the total energy and possibly of the membrane energy, of the energy of deflection, of the energy of shear and of the energy of membrane-bending coupling at the geometric location concerned:

INST	LIEU	ENTITE	TOTALE	MEMBRANE	FLEXION	CISAILLE	COUPL_MF
INST	LIEU	ENTITE	TOTALE	MEMBRANE	FLEXION	CISAILLE	COUPL_MF
1.00000E+00	MA	TOUT	4.00093E+12	0.00E+00	0.00E+00	0.00E+00	0.00E+00
2.00000E+00	GMA1	GROUP_MA	2.71323E+11	0.00E+00	0.00E+00	0.00E+00	0.00E+00
2.00000E+00	GMA2	GROUP_MA	2.71323E+11	0.00E+00	0.00E+00	0.00E+00	0.00E+00
2.00000E+00	UNION_GROUP_MA	GROUP_MA	5.42646E+11	0.00E+00	0.00E+00	0.00E+00	0.00E+00

Membrane, flexure, shear, and membrane—flexure coupling energies are available when the geometric locus contains plate or shell elements. The shear and membrane—flexure coupling energies are calculated only when the result concept is of the evol_elas type, otherwise they are set to 0.

Note: If there is more than one group of elements in the list, then a row is added to the output table which is the result on the union of the cells of the given groups in addition to the result per group. This new line corresponds to the group of elements” UNION_GROUP_MA “.

3.12. Keyword ENER_ELTR#

3.12.1. But#

Allows you to calculate the elastic tensile deformation energy for each moment \(t\) after an elastic or elastoplastic calculation, on the topological selection chosen by the user.

The user can carry out this post-processing based on a result concept such as evol_noli or evol_elas. It is important to note that this option is only available in small deformations. In the case of an evol_noli concept, the calculation performed must use (DEFORMATION = PETIT).

Only in small deformations (DEFORMATION = PETIT), the calculation is carried out using this expression:

\({E}_{\mathit{el}}^{\mathit{traction}}(t)={\int }_{v}^{t}\frac{\mathrm{\lambda }}{2}H(\mathit{tr}(\mathrm{\epsilon }(t)))\mathit{tr}{(\mathrm{\epsilon }(t))}^{2}+\mathrm{\mu }\sum _{i=1}^{3}H({\mathrm{\epsilon }}_{i}(t)){\mathrm{\epsilon }}_{i}{(t)}^{2}\mathit{dv}\)

where \(H\) represents the Heaviside function,

\(\mathrm{\epsilon }\) represents the elastic deformation tensor,

\({\mathrm{\epsilon }}_{i}\) represents the main elastic deformations.

3.12.2. Syntax#

| ENER_ELTR=_F (
♦/TOUT = 'OUI',
/GROUP_MA = lgrma, [l_gr_mesh]
)

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
◊ CARA_ELEM = carac, [cara_elem]
◊ | LAYER_NUMBER =
| LAYER_LEVEL =
◊ MODE_FOURIER =
♦ RESULTAT =

3.12.3. Operands#

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

3.12.4. Table produced#

The table contains, for each moment, the values of the elastic tensile energy (TOTALE):

INST	LIEU	ENTITE	TOTALE
INST	LIEU	ENTITE	TOTALE
1.00000E+00	MA	TOUT	4.00093E+12
2.00000E+00	GMA1	GROUP_MA	2.71323E+11
2.00000E+00	GMA2	GROUP_MA	2.71323E+11
2.00000E+00	UNION_GROUP_MA	GROUP_MA	5.42646E+11

3.13. Keyword ENER_TOTALE#

3.13.1. But#

Key word: factor used to calculate the total deformation energy for 2D or 3D continuous media elements.

For behaviors VMIS_ISOT_LINE or VMIS_ISOT_TRAC (isotropic work hardening), the energy is calculated from the stress fields, internal variables and the material:

\({E}^{T}={E}^{\mathrm{el}}+{E}^{p}=\frac{1}{2}{\int }_{v}{\sigma }^{T}{A}^{-1}\sigma \mathrm{dv}+{\int }_{v}({\int }_{0}^{p}R(q)\mathrm{dq})\mathrm{dv}\)

being the cumulative equivalent plastic deformation.

With option SIMO_MIEHE, this energy applies to the two models VMIS_ISOT_LINE or VMIS_ISOT_TRAC:

\({E}^{T}={\int }_{{v}_{0}}\left({\rho }_{0}\Psi +{\int }_{0}^{t}\Delta d\tau \right)\mathit{dv}\)

where \(\Psi\) and \(\Delta\) are the free energy and the dissipation potential respectively, \({V}_{0}\) the initial volume.

For more details, see [R5.03.21].

For the other behaviors, the energy is obtained by incremental integration:

\({E}^{T}={\int }_{v}\left({\int }_{0}^{t}\mathrm{\sigma }\mathrm{.}d\mathrm{\epsilon }\right)\mathit{dv}\)

Incremental integration using the trapezius method involves:

that the discretization in time is sufficiently fine,
that the initial stresses and deformations are zero,
and that the calculation is requested from the first moment of calculation.

3.13.2. Syntax#

| ENER_TOTAL= _F (
♦/TOUT = 'OUI',
/GROUP_MA = lgrma, [l_gr_mesh]
)

Simple keywords: (see [§2)

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
◊ CARA_ELEM = carac, [cara_elem]
◊ | LAYER_NUMBER =
| LAYER_LEVEL =
◊ MODE_FOURIER =
♦ RESULTAT =

3.13.3. Operands#

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

3.13.4. Table produced#

The table contains, for each moment, the values of the total energy at the geometric location concerned:

INST	LIEU	ENTITE	TOTALE
INST	LIEU	ENTITE	TOTALE
1.00000E+00	MA	TOUT	4.00093E+12
2.00000E+00	GMA1	GROUP_MA	2.71323E+11
2.00000E+00	GMA2	GROUP_MA	2.71323E+11
2.00000E+00	UNION_GROUP_MA	GROUP_MA	5.42646E+11

3.14. Keyword WEIBULL#

3.14.1. But#

Keyword allowing, for each defined moment, the calculation of the elementary field of power

of the Weibull stress whose expression on the \(K\) mesh is given, without taking into account the plastic deformation, by:

\({\sigma }_{w}^{m}(K)=\frac{1}{{V}_{\mathrm{ref}}}{\int }_{{K}_{p}}{\sigma }_{1}^{m}d{K}_{p}\)

and, taking into account plastic deformation by:

\({\sigma }_{w}^{m}(K)=\frac{1}{{V}_{\mathrm{ref}}}{\int }_{{K}_{p}}{\sigma }_{1}^{m}\mathrm{exp}(\frac{-m}{2}{\varepsilon }_{1}^{p})d{K}_{p}\)

\({K}_{p}\) refers to the part of the \(K\) mesh that has plasticized, that is, the part of \(K\) where the cumulative plastic deformation exceeds a certain threshold; \({\sigma }_{1}\) represents the maximum principal stress and \({\varepsilon }_{1}^{p}\) represents the maximum principal plastic deformation.

The material parameters \(m\), \({V}_{\mathrm{ref}}\) and the plasticity threshold are defined in DEFI_MATERIAU by the behavior relationship WEIBULL (cf. [R7.02.06]).

Once this elementary field has been determined, the option calculates by « summation » the Weibull constraint of a domain \(D\) for each defined moment:

\({\sigma }_{w}(D)={(C\underset{K\in D}{\Sigma }{\sigma }_{w}^{m}(K))}^{\frac{1}{m}}\)

where

is a coefficient intended to take into account the symmetries (bi- and three-dimensional cases) and the thickness (in the two-dimensional case) of the structure containing the domain

(keyword COEF_MULT).

The probability of breaking domain \(D\) is then calculated by:

\({P}_{w}(D)=1-\mathrm{exp}(-\frac{{\sigma }_{w}^{m}}{{\sigma }_{u}^{m}})\)

The parameter « cleavage constraint » \({\sigma }_{\mu }\) is also defined in the WEIBULL behavior relationship.

Finally, the previous expressions of Weibull stress and failure probability are only valid in the case of a monotonic loading path. However, this type of post-treatment can also be applied to a more general loading path, including when the cleavage stress depends on temperature (behavioral relationship WEIBULL_FO). The expressions of the Weibull constraint and the probability of rupture are then different (cf. [R7.02.06]).

Note:

For the factor keyword WEIBULL, the model and material field are mandatory (unless RESULTATest present) .

Tips for using this model are given in the documentation [U2.05.08].

Only the moments defined by the user using the keywords INST/NUME_ORDRE are taken into account in calculating the maximum constraints on the history. To take into account all the moments, use TOUT_ORDRE = « OUI ».

3.14.2. Syntax#

| WEIBULL = _F (
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgrma, [l_gr_mesh]
    ◊ OPTION =/'SIGM_ELGA', [DEFAUT]
    /'SIGM_ELMOY',
    ◊ CORR_PLAST =/'OUI',
    /'NON', [DEFAUT]
    ◊ COEF_MULT =/key, [R]
    /1., [DEFAUT]
)

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = field, [field master]

    ◊ CARA_ELEM = carac, [cara_elem]
◊ | LAYER_NUMBER =
| LAYER_LEVEL =
◊ MODE_FOURIER =
♦/CHAM_GD =
/RESULTAT =

3.14.3. Operands#

3.14.3.1. Operand OPTION#

◊/OPTION = 'SIGM_ELGA',

The value of the elementary field associated with cell \(K\) is obtained by integration by quadrature at the Gauss points of the expression \(\frac{1}{{V}_{p}}{\int }_{{K}_{p}}{\sigma }_{1}^{m}\mathrm{dK}\).

/OPTION = “SIGM_ELMOY”,

The value of the elementary field associated with mesh \(K\) is obtained from the maximum main value of the \(\frac{1}{{V}_{p}}{\int }_{{K}_{p}}\sigma \mathrm{dK}\) tensor, whose value is approximated by quadrature at the Gauss points.

3.14.3.2. Operand CORR_PLAST#

◊/CORR_PLAST = 'OUI',

The Weibull stress field is evaluated taking into account plastic deformation.

/CORR_PLAST = 'NON',

The Weibull stress field is evaluated without taking into account plastic deformation.

3.14.3.3. Operand COEF_MULT#

/COEF_MULT = value,

The default value for this coefficient is \(1.0\).

The following table, in which the thickness is noted \(e\), indicates typical values of the \(C\) coefficient as a function of the type of symmetry:

simple symmetry: the plane of symmetry of the mesh passes through the plane of the defect and the defect is entirely meshed,
double symmetry: the plane of symmetry of the mesh also passes through the plane of the defect but only one half of the defect is meshed.

	3D and 3D_SI	AXIS and AXIS_SI **	D_ PLAN and D_ PLAN_SI**	C_ PLAN
SIMPLE	2	\(4\pi\)		\(2e\)	\(2e\)
DOUBLE	4	not applicable	not applicable	not applicable	not applicable
NON	1	\(2\pi\)		\(e\)	\(e\)

Symmetry-Thickness Multiplier Values

3.14.4. Table produced#

The table contains, for each moment, the values of the Weibull constraint, the probability of failure, and the power

of the Weibull constraint on the geometric location concerned:

INST	ENTITE	SIGMA_WEIBULL	PROBA_WEIBULL	SIGMA_WEIBULL **M

00000E+00	TOUT	2.49298E+02	0.00E+00	3.32096E+57
2.00000E+00	TOUT	2.50473E+02	0.00E+00	3.71756E+57

3.15. Keyword RICE_TRACEY#

3.15.1. But#

This option allows, for each defined calculation instant \({t}_{n}\), the calculation of the growth rate \(\frac{R({t}_{n})}{-{R}_{0}}\) of a spherical cavity with respect to a domain (\(D(R({t}_{n}))\) and \({R}_{0}\) designate respectively the current radius and the initial radius of the cavity). The Rice-Tracey law of evolution is expressed by the relationship:

\(\frac{d}{\mathrm{dt}}\mathrm{log}(\frac{R}{{R}_{0}})=0.283\mathrm{Signe}(\frac{{\sigma }_{M}}{{\sigma }_{\mathrm{eq}}})\mathrm{exp}(∣\frac{2{\sigma }_{M}}{2{\sigma }_{\mathrm{eq}}}∣)\frac{d{\varepsilon }_{\mathrm{eq}}^{p}}{\mathrm{dt}}\)

(\({\sigma }_{M}=\frac{1}{3}\mathrm{Trace}(\sigma )\); \({\sigma }_{\mathrm{eq}}\) refers to the equivalent von Mises stress and \({\varepsilon }_{\mathrm{eq}}^{p}\) refers to the equivalent von Mises strain).

3.15.2. Syntax#

| RICE_TRACEY = _F (
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgrma, [l_gr_mesh]
    ◊ OPTION =/'SIGM_ELGA', [DEFAUT]
    /'SIGM_ELMOY',
    ◊ LOCAL =/'OUI', [DEFAUT]
    /'NON',
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]

    ◊ CARA_ELEM = carac, [cara_elem]
◊ | LAYER_NUMBER =
| LAYER_LEVEL =
◊ MODE_FOURIER =
♦/CHAM_GD =
/RESULTAT =

3.15.3. Operands#

3.15.3.1. Operand OPTION#

◊ OPTION =/'SIGM_ELGA', [DEFAUT]

The elementary fields of stresses and plastic deformations are used in their representations at Gauss points.

/'SIGM_ELMOY',

The elementary fields of the stresses and the plastic deformations are averaged with respect to the Gauss points before being used.

3.15.3.2. Operand LOCAL#

◊ LOCAL =/'OUI', [DEFAUT]

The Rice-Tracey law is integrated into each cell \(K\) of the domain \(D\) and the result consists of the maximum value obtained over all the cells in the domain.

/'NON',

The fields of triaxiality \(\frac{{\sigma }_{M}}{{\sigma }_{\mathrm{eq}}}({t}_{n})\) and the variation of plastic deformation \(\Delta {\varepsilon }_{\mathrm{eq}}^{p}({t}_{n})\) are calculated on each mesh. Then, their respective averages, weighted by the volume of the cells in the domain, are determined. Finally, the Rice-Tracey law is integrated into these averaged values.

3.15.3.3. Operands TOUT/GROUP_MA#

Compute domain (s) \(D\) are specified by:

/TOUT = 'OUI',

A single domain is defined, it coincides with the entire structure.

/GROUP_MA = lgrma,

Each group of elements in the LGRM list defines a calculation domain.

3.15.4. Table produced#

The table contains, for each moment, the values of the growth rate of a spherical cavity and of the volume concerned at the geometric location concerned:

INST	LIEU	TX_CROIS_CAVITES	VOLUME_CONCERNE

00000E+00	MA101	1.00000E+00	3.75000E+00
2.00000E+00	MA101	1.00000E+00	6.23719E-01

3.16. Keyword INDIC_ENER#

3.16.1. But#

Keyword factor for calculating an overall indicator of loss of proportionality of elastoplasticity loading, based on energy density. This indicator is described in detail in document [R4.20.01].

We recall its function and its expression. This indicator is intended to detect whether, during the history of the structure and up to the current moment t, and for an area of the structure chosen by the modeler, there has been a loss of proportionality of the load (i.e. it is a question of having an overall measure of the change in the main directions of the stress tensor for each point in the zone defined by the user).

This indicator can only be used for models whose material has isotropic work hardening and whose elements are 2D or 3D isoparametric.

The expression for this indicator is:

\(I=\frac{1}{V}\underset{V}{\int }(1-\frac{\underline{\Psi }}{\Omega })\mathrm{dv}\)

where:

\(V\) is the volume of the domain defined by the user,
\(\underline{\Psi }\) is the total elastic energy density associated with the tensile curve if we consider the non-linear elastic material.

More exactly, his expression is as follows:

\(\begin{array}{ccc}\underline{\Psi }=\frac{1}{2}K\cdot {\mathrm{tr}}^{2}(\varepsilon )+\frac{2\mu }{3}{\varepsilon }_{\mathrm{eq}}^{2}& \mathrm{si}& {\sigma }_{\mathrm{eq}}<R(p)\\ \underline{\Psi }=\frac{1}{2}K\cdot {\mathrm{tr}}^{2}(\varepsilon )+\frac{{R}^{2}(p)}{6\mu }+\underset{0}{\overset{p}{\int }}R(s)\mathrm{ds}& \mathrm{si}& {\sigma }_{\mathrm{eq}}=R(p)\end{array}\)

where:

\(K\) is the compressibility module,
\(\mu\) is the Lamé shear coefficient,
\(R(p)\) is the threshold of the traction curve associated with the cumulative plastic deformation \(p\),
\(\Omega\) is the deformation energy density defined by:

\(\Omega (t)=\underset{0}{\overset{t}{\int }}\sigma \cdot \dot{\varepsilon }d\tau\)

we can break \(\Omega (t)\) down into an elastic part and a plastic part:

\(\Omega (t)={\Omega }_{\mathrm{élas}}(t)+{\Omega }_{\mathrm{plas}}(t)\)

with:

\(\begin{array}{}{\Omega }_{\mathrm{élas}}(t)=\frac{1}{2}\sigma \cdot {\varepsilon }^{\mathrm{élas}}\\ {\Omega }_{\mathrm{plas}}(t)=\underset{0}{\overset{t}{\int }}R(p)\mathrm{dp}\end{array}\)

Note:

In the case where we have \(\Omega (t)=0\) , we pose \(I=0\) .

3.16.2. Syntax#

| INDIC_ENER = _F (
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgrma, [l_gr_mesh]
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
♦ RESULTAT = resu, [evol_noli]

3.16.3. Operands#

The indicator is calculated on the domain defined by the keywords:

/TOUT = 'OUI',

On all elements of the mo model.

/GROUP_MA = lgrma,

On the lgrma list of mesh groups for the mo model. If there is more than one group of elements in the list, then a row is added to the output table which is the result on the union of the cells of the given groups in addition to the result per group. This new line corresponds to the group of elements” UNION_GROUP_MA “.

3.16.4. Table produced#

The table contains, for each moment, the value of the global indicator of the loss of proportionality of the elastoplasticity load at the geometric location in question:

INST	LIEU	INDIC_ENER

00000E+00	MA	4.77299E-02
2.00000E+00	MA	3.33763E-02

Note: If there is more than one group of elements in the list, then a row is added to the output table which is the result on the union of the cells of the given groups in addition to the result per group. This new line corresponds to the group of elements” UNION_GROUP_MA “.

3.17. Keyword INDIC_SEUIL#

3.17.1. But#

Key word: factor used to calculate an overall indicator of loss of proportionality of elastoplasticity loading.

This indicator makes it possible, on the one hand, to know, on average over the zone in question, whether the stress tensor and that of the plastic deformations have the same directions and if the plastic threshold has been reached at the current moment, and on the other hand if, during the course of history, the plastic deformation has changed direction.

The expression for this indicator is:

\(I=\frac{1}{V}\underset{V}{\int }(1-\frac{\sigma \cdot {\varepsilon }^{p}}{R(p)\cdot p})\mathrm{dv}\)

where:

\(V\) is the volume of the domain defined by the user,
\(\sigma\) is the stress tensor at the current moment,
\({\varepsilon }^{p}\) is the tensor of plastic deformations at the current moment,
\(R(p)\) is the work hardening function (with \(R(o)={\sigma }_{y}\) where \({\sigma }_{y}\) is the elastic limit).

i.e. it is the threshold of the traction curve associated with the cumulative plastic deformation \(p\).

\(p\) is the cumulative plastic deformation.

Note:

In the case where we have \(R(p)\cdot p=0\) , we pose \(I=0\) .

The dot product \(\sigma \cdot {\varepsilon }^{p}\) is associated with the norm in the sense of von Mises.

This indicator is standardized and has a value between 0 and 1.

It is void if the load has maintained its proportionality at each point of \(V\) throughout the past story.

This indicator is described in detail in document [R4.20.01].

3.17.2. Syntax#

| THRESHOLD_INDEX = _F (
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgrma, [l_gr_mesh]
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
♦ RESULTAT = resu, [evol_noli]

3.17.3. Operands#

The indicator is calculated on the domain defined by the keywords:

/TOUT = 'OUI',

On all elements of the mo model.

/GROUP_MA = lgrma,

3.17.4. Table produced#

The table contains, for each moment, the value of the global indicator of the loss of proportionality of the elastoplasticity load at the geometric location in question:

INST	LIEU	INDIC_SEUIL

00000E+00	MA	4.77299E-02
2.00000E+00	MA	3.33763E-02

Note: If there is more than one group of elements in the list, then a row is added to the output table which is the result on the union of the cells of the given groups in addition to the result per group. This new line corresponds to the group of elements” UNION_GROUP_MA “.

3.18. Keyword CHAR_LIMITE#

3.18.1. But#

Post-processing of the limit load calculation [R7.07.01 §2.3].

This keyword factor allows the calculation of the limit load of a structure using a kinematic approach. Its use requires first to have carried out a non-linear calculation (see operator STAT_NON_LINE [U4.51.03]) filled in with the keyword RESULTAT and whose characteristics are as follows:

law of behavior NORTON_HOFF,
increasing list of calculation times corresponding to regularization values of the law of NORTON_HOFF that tend to 1 (in practice, it is recommended to limit yourself to moments between 1 and 2 which do not lead to calculations that are too long while making it possible to obtain an upper bound of the limit load that is sufficiently precise),
controlled (unitary) load corresponding to the load in relation to which the limit load is sought to be estimated, the control method being TYPE =” ANA_LIM “,
possibly a loading that is constant, the existence of which must then be remembered by the keyword CHAR_CSTE =” OUI “.

The operator POST_ELEM then produces a table which gives, for each moment of the calculation, that is to say for increasingly weaker regularizations, an upper bound CHAR_LIMI_SUP of the limit load supported by the structure. Furthermore, in the absence of a constant load, CHAR_CSTE = “NON”, the table also contains an estimate CHAR_LIMI_ESTIM of a lower bound of the limit load. On the other hand, if a constant loading is present, CHAR_CSTE = “OUI”, such an estimate of the lower bound is no longer available but the table then contains the power PUIS_CHAR_CSTE of the constant loading in the speed field solution of the problem.

A detailed example of limit load calculation is provided in [U2.05.04].

3.18.2. Syntax#

| CHAR_LIMIT = _F (
    ◊ CHAR_CSTE =/'NON', [DEFAUT]
    /'OUI',
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
♦ RESULTAT = resu, [evol_noli]
◊ CARA_ELEM = carac, [cara_elem]
◊ MODE_FOURIER = h, [I]

3.18.3. Operands#

◊ CHAR_CSTE =/'NON', [DEFAUT]
/'OUI',

A keyword that indicates whether the load is constant or not constant (value by default).

3.18.4. Table produced#

The table contains, if CHAR_CSTE = “OUI”:

INST	CHAR_LIMI_SUP	PUIS_CHAR_CSTE

00000E+00	1.46838E+01	-2.50000E-01
2.00000E+00	1.46838E+01	-2.50000E-01

The table contains, if CHAR_CSTE = “NON”:

INST	CHAR_LIMI_SUP	CHAR_LIMI_ESTIM

00000E+00	1.46838E+01	-2.50000E-01
2.00000E+00	1.46838E+01	-2.50000E-01

3.19. Keyword CARA_GEOM#

3.19.1. But#

CARA_GEOM is used by the MACR_CARA_POUTRE [U4.42.02] macrocommand to calculate the geometric characteristics (center of inertia, moments of inertia) of a meshed beam section in 2D continuous medium elements.

3.19.2. Syntax#

| CARA_GEOM = _F (
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgma, [l_gr_mesh]
    ◊ SYME_X =/'OUI',
    /'NON', [DEFAUT]
    ◊ SYME_Y =/'OUI',
    /'NON', [DEFAUT]
    ◊ ORIG_INER = (xp, yp), [L_r]
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]

3.19.3. Operands#

3.19.3.1. Operands TOUT/GROUP_MA#

Define the location of the calculation. In particular, it is possible to calculate the characteristics for a set of cells, defined by GROUP_MA.

3.19.3.2. Operands SYME_X/SYME_Y#

Taking into account symmetry with respect to \(X\) or \(Y\) (or both). The mesh provided by the user then corresponds to half of the section (or a quarter).

3.19.3.3. Operand ORIG_INER#

Allows you to give the coordinates of a point in relation to which the geometric characteristics will be calculated [U4.42.02].

3.19.4. Table produced#

See [U4.42.02] §3.2

3.20. Keyword CARA_POUTRE#

3.20.1. But#

Note

This keyword is not intended to be called directly by the user.

CARA_POUTRE is used exclusively by the MACR_CARA_POUTRE [U4.42.02] macro-command to calculate the mechanical characteristics (torsional constant, torsional radius, shear constants, shear center position, warping constant) of a meshed section in 2D elements.

Its use requires the prior call of numerous commands, specific to each calculated option. The operands will therefore not be detailed here. For more details, refer to MACR_CARA_POUTRE [U4.42.02].

3.20.2. Syntax#

| CARA_BEAM = _F (
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgma, [gr_mesh]
    ◊ GROUP_MA_INTE = lgma_inte, [l_gr_mesh]
    ◊ CARA_GEOM = tab, [tabl_cara_geom]
    ◊ LAPL_PHI = :math:`\Delta \Phi`, [evol_ther]
    ◊ LAPL_PHI_Y = :math:`\Delta \Phi y`, [evol_ther]
    ◊ LAPL_PHI_Z = :math:`\Delta \Phi z`, [evol_ther]
    ◊ RT = rt, [R]
    ◊ ♦ LIAISON =/'ROTULE',
    /'ENCASTREMENT',
    ♦ LONGUEUR = L, [R]
    ♦ MATERIAU = mat, [subdue]
    ◊ OPTION =/'CARA_TORSION',
    /'CARA_CISAILLEMENT',
    /'CARA_GAUCHI',
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]

◊ CHAM_MATER = tamer, [chamber_master]

3.20.3. Table produced#

See [U4.42.02] §3.2

3.21. Keyword AIRE_INTERNE#

3.21.1. But#

Keyword factor allowing the calculation of the area of a hole in a 2D mesh from its outline.

3.21.2. Syntax#

| INTERNAL_AREA = _F (♦ GROUP_MY_EDGE = lgma)

Simple keyword:

◊ MODELE = mo, [model]

3.21.3. Operand#

♦ GROUP_MA_BORD = lgma,

List of edge mesh groups delimiting the hole (SEG2 or SEG3)

3.21.4. Table produced#

The table contains, for each group of edge elements, the area of the hole and the length of its outline.

GROUP_MA	AIRE	LONGUEUR

GMA1	3.14128E-02	6.28303E-01
GMA 2	3.14128E-02	6.28303E-01

3.22. Keyword TRAV_EXT#

3.22.1. But#

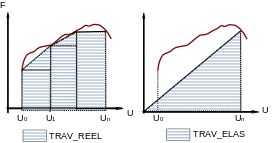
Keyword factor used to calculate the work of real external forces TRAV_REEL or elastic TRAV_ELAS as defined below:

\(\text{TRAV\_REEL}\mathrm{=}\underset{{t}_{0}}{\overset{t}{\mathrm{\int }}}\underset{\Omega }{\mathrm{\int }}\sigma \mathrm{\cdot }\dot{\varepsilon }\mathrm{=}\underset{{t}_{0}}{\overset{t}{\mathrm{\int }}}{\mathrm{F}}_{\text{int}}\mathrm{\cdot }\dot{\mathrm{U}}\) eq 3.22.1-1

\(\text{TRAV\_ELAS}=\frac{1}{2}\underset{\Omega }{\int }\sigma \cdot \varepsilon =\frac{1}{2}{F}_{\text{int}}\cdot U\)

eq 3.22.1-2

The calculation is carried out on the basis of a result SD, entered under the keyword RESULTAT, for which the nodal forces, i.e. the internal forces, were previously calculated by the operator CALC_CHAMP, option “FORC_NODA” [U4.81.04]. In the case of real work, the initial instant \({t}_{0}\) corresponds to the first instant archived in the result SD; the integration in time is carried out by a trapezius method:

\(\begin{array}{}\text{TRAV\_REEL}=\sum _{i=0}^{n-1}\underset{{t}_{i}}{\overset{{t}_{i+1}}{\int }}F(U({t}_{i}))\mathrm{.}U({t}_{i})\mathrm{dt}=\sum _{i=0}^{n-1}\underset{{U}_{i}}{\overset{{U}_{i+1}}{\int }}F(Z)\mathrm{dZ}\approx \frac{1}{2}\sum _{i=0}^{n-1}({U}_{i+1}-{U}_{i})({F}_{i+1}+{F}_{i})\\ \approx \frac{1}{2}\sum _{i=0}^{n-1}({U}_{i+1}\mathrm{.}{F}_{i+1}+{U}_{i+1}\mathrm{.}{F}_{i}-{U}_{i}\mathrm{.}{F}_{i+1}-{U}_{i}\mathrm{.}{F}_{i})\end{array}\)

The two quantities TRAV_REEL and TRAV_ELAS are calculated for each instant archived in the result SD.

These quantities can be interpreted graphically on the force-displacement response curve of the structure (provided that the force is dual of the displacement, for example the pressure and the volume in the case of a cavity under pressure).

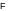
3.22.2. Syntax#

TRAV_EXT = _F ()

Simple keyword:

♦ RESULTAT = resu/[evol_elas]
                            /[evol_noli]
                            /[dyna_trans]

Name of the data structure that was calculated as the result of the calculation.

3.22.3. Table produced#

The table contains, for each moment, elastic work and the work of real external forces.

INST	TRAV_ELAS	TRAV_REEL

0.00000E+00	1.16070E+00	1.16070E+00
1.00000E+00	4.64279E+00	4.64279E+00

3.23. Operand INTEGRALE#

3.23.1. But#

Allows you to calculate the integral of a component of a field on a domain defined by the keywords TOUT, GROUP_MA.

A table is produced containing the value of the integral as well as the mean (equal to the integral divided by the volume).

This feature is forbidden for structural elements except for components N, VY, VY, VZ, MT, MFYet MFZsur the elements POU_D_T.

3.23.2. Syntax#

| INTEGRAL =_F (
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgrma, [l_gr_mesh]
    ◊ NOM_CMP = nocmp, [Kn]
    ◊ NOM_VARI = novari, [Kn]
    ♦ TYPE_MAILLE = /'1D',

        /'2D',
    /'3D',
    ◊ DEJA_INTEGRE =/'OUI'
    /'NON'
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
♦/CHAM_GD = cham, [cham_gd]

    /RESULTAT = resu, [result]

/NOM_CHAM = field, [Kn]

# selection of calculation times

see TOUT_ORDRE, NUME_ORDRE, LIST_ORDRE, INST, LIST_INST in [U4.71.00]

3.23.3. Operands#

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

♦ TYPE_MAILLE

Allows you to filter according to the size of the meshes

(mandatory in order to ensure the homogeneity of the meshes in size).

◊ DEJA_INTEGRE = /' OUI '

                    /' NON '

Only used for element-wise constants. In this case, this keyword is mandatory and is used to differentiate between really constant fields and fields integrated into the element (such as potential or kinetic energies for example). This distinction is important for calculating the integral because we do not make the same « sum ».

◊ NOM_CMP = nocmp, [Kn]

Name of the component whose integral we want to calculate.

◊ NOM_VARI = novari, [Kn]

For the internal variable fields (VARI_ *), you can give the name of the internal variable whose integral you want to calculate (see [U4.51.11] for the rules for naming internal variables).

3.23.4. Table produced#

The table contains, for each moment, the integral and the mean:

INST	INTE_PRES	MOYE_PRES

0.00000E+00	1.16070E+00	1.16070E+00
1.00000E+00	4.64279E+00	4.64279E+00

Note:: If there is more than one group of elements in the list, then a row is added to the output table which is the result on the union of the cells of the given groups in addition to the result per group. This new line corresponds to the group of elements” UNION_GROUP_MA “.

3.24. Operand MINMAX#

3.24.1. But#

Allows you to calculate the extremes in space of a list of components of a field, for all the times specified on a domain defined by the keywords TOUT, GROUP_MA.

A table is produced containing the value of the min, the max, and their location: name of the mesh and of the Gauss point, name of the node.

3.24.2. Syntax#

MINMAX = _F (
♦/TOUT = 'OUI',
/GROUP_MA = lgrma, [l_gr_mesh]
◊ MODELE = mo, [model]
♦/CHAM_GD = cham, [cham_gd]

    /RESULTAT = resu, [result]

        NOM_CHAM = field, [Kn]

    # selection of calculation times

see TOUT_ORDRE, NUME_ORDRE, LIST_ORDRE, INST, LIST_INST in [U4.71.00]

♦ NOM_CMP = lcmp)

3.24.3. Operands#

♦/TOUT = 'OUI',

Calculation of the extremes over the entire structure.

/GROUP_MA = lgrma,

Calculation of the extremes on a list of groups of elements, If there is more than one group of elements in the list, then a row is added to the output table which is the result on the union of the cells of the given groups in addition to the result per group. This new line corresponds to the group of elements” UNION_GROUP_MA “

3.24.4. Table produced#

The table contains, for each moment, the max and min values for each component as well as their location:

CHAM_GD	INST	MAX_EPXX	MA_MAX_EPXX	PT_MAX_EPXX

EPMAX	0.0	6.90232E+02	M121 ROAD	4

MIN_EPXX	MA_MIN_EPXX	PT_MIN_EPXX
0.00000E+00	M1080	1


Note: If there is more than one group of elements in the list	then a row is added to the output table which is the result on the union of the cells of the given groups in addition to the result per group. This new line corresponds to the group of elements” UNION_GROUP_MA “.

3.25. Keyword ENER_DISS#

3.25.1. But#

Allows you to calculate the dissipation energy (integral over the energy density domain DISS_ELGA calculated by CALC_CHAMP). For the time being, this option can only be calculated in the following case:

element DKTG and GLRC_DM and DHRC behavior laws.

3.25.2. Syntax#

| ENER_DISS=_F (
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgrma, [l_gr_mesh]
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
◊ CARA_ELEM = carac, [cara_elem]
◊ | LAYER_NUMBER =
| LAYER_LEVEL =
♦ RESULTAT =

3.25.3. Operands#

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

3.25.4. Table produced#

The table contains, for each moment, the values of the dissipation energy at the geometric location concerned:

INST	LIEU	ENTITE	TOTALE
1.00000E+00	MA	TOUT	4.00093E+12
2.00000E+00	GMA1	GROUP_MA	2.71323E+11
2.00000E+00	GMA2	GROUP_MA	2.71323E+11
2.00000E+00	UNION_GROUP_MA	GROUP_MA	5.42646E+11

note: If there is more than one group of elements in the list, then a row is added to the output table which is the result on the union of the cells of the given groups in addition to the result per group. This new line corresponds to the group of elements” UNION_GROUP_MA “.

3.26. Operand VOLUMOGRAMME#

3.26.1. But#

Allows you to calculate the surface or volume distribution of the value of a component of a field at different times on a domain defined by the keywords TOUT or GROUP_MA.

A table is produced containing:

the limits of the intervals defined by the minimum and maximum values of the component and the number of intervals desired,
the percentage of the structure corresponding to each interval.

Note

The number of intervals is defined by the user, the limits are determined by Code_Aster as follows:

Let be \(n\) the number of intervals, and \(\mathrm{Vmin}\) and \(\mathrm{Vmax}\) the extreme values of the component.

Be \(p=(\mathrm{Vmax}-\mathrm{Vmin})/n\) the length of each interval.

The intervals are:

\([\mathrm{Vmin},\mathrm{Vmin}+p],[\mathrm{Vmin}+p,\mathrm{Vmin}+\mathrm{2p}],\mathrm{...},[\mathrm{Vmin}+(n-1)p,\mathrm{Vmax}]\)

3.26.2. Syntax#

| VOLUME CHART =_F (
♦/TOUT = 'OUI',
/GROUP_MA = grma, [gr_mesh]
◊ TYPE_MAILLE = /'2D',
/'3D',
◊ NOM_CHAM = field, [Kn]
♦ NOM_CMP = cmp, [Kn]
◊ BORNES = (bmin, bmax), [L_r]
◊ NORME = /' RELATIF '[default]
/' ABSOLU '
◊ | NB_INTERV = nb_int [I]
| THRESHOLD = threshold [R]
)

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
◊ CARA_ELEM = carac, [cara_elem]
♦/CHAM_GD = cham, [cham_gd]

    /RESULTAT = resu, [result]

# selection of calculation times

see TOUT_ORDRE, NUME_ORDRE, LIST_ORDRE, INST, LIST_INST in [U4.71.00]

3.26.3. Operands#

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

On a group of elements.

◊ TYPE_MAILLE

Allows you to filter according to the size of the meshes.

◊ | NB_INTERV = nb_int [I]

Number of intervals desired

| THRESHOLD = threshold [R]

Allows you to choose a threshold. In this case the number of intervals is equal to two.

◊ NORME = /' RELATIF '[default]
                            /' ABSOLU '

With NORME =” RELATIF “, the results displayed in column DISTRIBUTION of the produced table are percentages (between 0 and 100) of the total volume calculated.

With NORME =” ABSOLU “, we do not do this dimensionalization and the results shown are the effective volumes, interval by interval, expressed in the unit defined by the mesh.

◊ BORNES = (bmin, bmax), [L_r]

Allows you to limit the field values used for calculating the volume chart.

3.26.4. Table produced#

The table contains the limits of the intervals and the percentage of the structure corresponding to each interval.

INST	NOM_CMP	GROUP_MA	BORNE_INF	BORNE_SUP	DISTRIBUTION

00000E+00	M 11	GAUCHE	-9.99990E-07	-8.99947E-07	1.95000E+01
00000E+00	M 11	GAUCHE	-8.99947E-07	-7.99947E-07	000 00E+0 1
00000E+00	M 11	GAUCHE	-7.99947E-07	6.99947E-07	0 5 0 00E+0 1

3.27. Operand NORME#

3.27.1. But#

Allows you to calculate the norm of a field on a domain defined by the keywords TOUT, GROUP_MA for continuous middle elements only. Currently, we can calculate the \({L}_{2}\) norm and the Frobenius norm (see the documentation for CALC_CHAMP).

A table containing the norm of the field is produced.

3.27.2. Syntax#

| STANDARD =_F (
    ◊ TYPE_NORM = |'L2', [Kn]
    |'FROBENIUS'
    ♦/TOUT = 'OUI',
    /GROUP_MA = lgrma, [l_gr_mesh]
    ◊ TYPE_MAILLE =/'2D', [Kn]
    /'3D',
    ♦ NOM_CHAM = field, [Kn]
    #Si CHAM_GD is complete
    ◊ COEF_MULT = key, [L_r]
    )

Simple keywords: (see [§2])

◊ MODELE = mo, [model]
◊ CHAM_MATER = tamer, [chamber_master]
♦/CHAM_GD = cham, [cham_gd]

    /RESULTAT = resu, [result]

# selection of calculation times

see TOUT_ORDRE, NUME_ORDRE, LIST_ORDRE, INST, LIST_INST in [U4.71.00]

3.27.3. Operands#

♦/TOUT = 'OUI',

Throughout the structure.

/GROUP_MA = lgrma,

On a list of groups of elements.

◊ TYPE_MAILLE

Allows you to filter according to the size of the meshes.

♦/CHAM_GD = cham, [cham_gd]

Accepted field fields are DEPL, TEMP,, NEUT_R,, FLUX, SIEF, and EPSI.

◊ COEF_MULT = key,

Allows you to give a list of real coefficients to weight the components of a field of type NEUT_R.

If this list is not indicated, these coefficients are set to 1.

If the size of this list is less than the number of components in the field, this list is supplemented by zero values.

3.27.4. Table produced#

The table contains the type of the standard (currently L2) and its value:

GROUP_MA	TYPE_NORM	VALE_NORM

GMA1	L2	4.64719E-03
GMA 2	L2	2.71323E -02

3.28. Operand TITRE#

◊ TITRE = you,

Title attached to the concept produced by this operator [U4.03.01].

3.29. Operand INFO#

◊ INFO =/1, [DEFAUT]
               /2,

Print setting.