3. Operands#

3.1. Keyword MONOCRISTAL#

An occurrence of the keyword factor MONOCRISTAL makes it possible to define a law of single-crystal elastoviscoplastic behavior. This must be repeated as many times as we have different monocrystalline behavior laws [R5.03.11].

3.1.1. Operand MATER#

Define the name of the material produced by DEFI_MATERIAU used for the single crystal. This operand makes it possible to verify that the parameters associated with the behaviors chosen under the keywords ECOULEMENT, ECRO_ISOT, ECRO_CINE and ELAS exist in the material.

3.1.2. Operand ECOULEMENT#

Define the type of viscoplastic flow used in the definition of the law of behavior MONOCRISTAL.

3.1.3. Operand ECRO_ISOT#

Defines the type of isotropic work hardening used in the definition of the law of behavior MONOCRISTAL.

3.1.4. Operand ECRO_CINE#

Defines the type of kinematic work hardening used in the definition of the law of behavior MONOCRISTAL.

3.1.5. Operand ELAS#

Defines the type of elastic behavior used in the definition of behavior law MONOCRISTAL.

3.1.6. Operand FAMI_SYST_GLIS#

Define the name of the family of sliding systems on which the MONOCRISTAL law of behavior has been defined. The orientations of the normals to the sliding planes and the sliding directions are automatically calculated by the code from the family name.

3.1.7. Operand TABL_SYST_GLIS#

Allows to provide a family of « user » sliding systems, read from a table. For each row of the table (corresponding to a sliding system), we must give the 3 components in the crystal coordinate system of the vectors \(n\) (normal to the sliding plane) and \(m\) (sliding direction). Example (see also the ssnd112c test):

\(\begin{array}{}{n}_{x}({s}_{1}),{n}_{y}({s}_{1}),{n}_{z}({s}_{1}),{m}_{x}({s}_{1}),{m}_{y}({s}_{1}),{m}_{z}({s}_{1})\\ {n}_{x}({s}_{2}),{n}_{y}({s}_{2}),{n}_{z}({s}_{2}),{m}_{x}({s}_{2}),{m}_{y}({s}_{2}),{m}_{z}({s}_{2})\\ \mathrm{etc...}\end{array}\)

Limitations: this feature is only active for behavior MONOCRISTAL, and provided you define a single system family (a single instance of MONOCRISTAL). It is not available for behavior POLYCRISTAL.

3.1.8. Operand MATR_INTER#

Allows to provide a (unique) interaction matrix between the sliding systems of a single crystal, read from a table. It is a square, symmetric table whose dimension is the number of total sliding systems. Example (see also the ssnd112c test):

Limitations: This feature is active for behavior MONOCRISTAL and for behavior POLYCRISTAL, as long as you only use one type of MONOCRISTAL).

3.1.9. Operand ROTA_RESEAU#

  • ROTA_RESEAU =” CALC “makes it possible to calculate the rotation of the crystal lattice and to take it into account in the resolution of the law of behavior MONOCRISTAL, implicitly only. The orientations of the normals to the sliding planes and the sliding directions are updated automatically by the code at each calculation moment, and the corresponding internal variables are added (see their meaning in [R5.03.11]).

  • ROTA_RESEAU =” POST “allows you to calculate the rotation of the crystal lattice, without taking it into account in the resolution, and to display the values in the internal variables, for post-processing purposes.

Validity and limitations:

This approximation is to be used in the presence of small deformations DEFORMATION =” PETIT “under COMPORTEMENT, for RELATION =” MONOCRISTAL” [U4.51.11]. It must therefore be used for moderate deformations (of the order of 10% at most). Beyond that, and to fully take into account the major deformations, it is necessary to use an adapted resolution, without using the keyword ROTA_RESEAU: DEFORMATION =” SIMO_MIEHE “in STAT_NON_LINE/COMPORTMENT.

3.2. Keyword POLYCRISTAL#

An occurrence of the keyword factor POLYCRISTAL makes it possible to define a phase of polycrystalline behavior, based on the data of a monocrystalline behavior, of the volume fraction of this phase, and of the orientation of this phase. This must be repeated as many times as there are different monocrystalline phases. In addition, a location rule, common to all phases, is defined by the keyword LOCALISATION [R5.03.11].

3.2.1. Operand MONOCRISTAL#

Defines the name of the compor data structure defining the single crystal, produced by a call prior to DEFI_COMPOR.

3.2.2. Operand FRAC_VOL#

Define the volume fraction of the current phase. The sum of all flight values must be equal to 1.

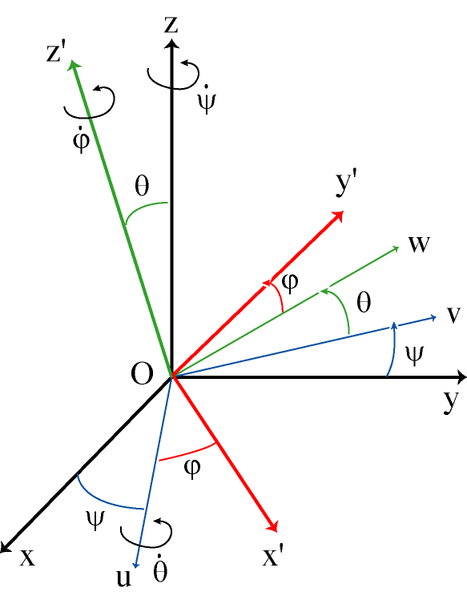
3.2.3. Operand ANGL_REP/ANGL_EULER#

Define the 3 nautical angles (provided in degrees) [U4.42.01] or the 3 Euler angles (provided in degrees) that allow the monocrystal to be oriented corresponding to the phase defined by the current occurrence of POLYCRISTAL. Euler angles are defined in a conventional way, we go from the fixed frame of reference \(Oxyz\) to the frame of reference linked to the solid \(Ox\text{'}y\text{'}z\text{'}\) by three successive rotations:

  • Precession \(\psi\), around the \(Oz\) axis, makes it possible to go from \(Oxyz\) to the reference frame \(Ouvz\).

  • Nutation \(\theta\), around the Ou axis, makes you want to go from \(Ouvz\) to \(Ouwz\text{'}\).

  • The proper rotation \(\varphi\), around the axis \(Oz\text{'}\), makes it possible to go from \(Ouwz’\) to the frame of reference linked to the solid \(Ox\text{'}y\text{'}z\text{'}\).

 _images/10000000000001D30000025832FF41BA23E00CF6.png

3.2.4. Keyword LOCALISATION#

Defines the name of the location rule used for the polycrystal.

3.2.5. Keyword MU_LOCA#

Define the \({\mu }^{\mathit{loca}}\) coefficient to be used in location rules.

3.2.6. DL and DA operands#

If the location rule is” BETA “, two real parameters must be provided: dl and da. The location rule is in [R5.03.11].

3.3. Keyword MULTIFIBRE#

This keyword makes it possible to associate incremental behavior with a group of fibers.

3.3.1. Operand GROUP_FIBRE#

Allows you to define, for each occurrence of the keyword factor MULTIFIBRE, the names of the fiber groups associated with the chosen behavior relationship. These fiber groups were previously defined by the command DEFI_GEOM_FIBRE, the resulting concept of which is specified by the GEOM_FIBRE keyword below.

3.3.2. Operand MATER#

This keyword makes it possible to specify the name of the material containing the parameters associated with the chosen behavior.

3.3.3. Operands RELATION#

These keywords make it possible to define the behavioral relationship associated with the fiber groups defined by GROUP_FIBRE. Behavioral relationships are described in [U4.51.11]. However, it should be noted that the list of behaviors that can be used with multifibre beams is restricted compared to [U4.51.11]. Allowed relationships are:

ELAS, CORR_ACIER, GRANGER_FP, GRAN_IRRA_LOG, MAZARS_UNIL,, VISC_IRRA_LOG, VMIS_CINE_GC, VMIS_CINE_LINE, VMIS_ISOT_LINE, VMIS_ISOT_TRAC.

3.3.4. Note on 1D behaviors#

The models of multifibre beams (such as those of bars, reinforcement grids) use unidirectional behaviour for each fibre. If the chosen law of behavior is available in 1D, this integration is used directly. Otherwise, the DEBORST method generalized to cases of 1D behaviors [R5.03.09] makes it possible to add the uniaxial constraint condition to all the behaviors available for 3D models under COMPORTEMENT (for more details see the documentation [R5.03.09]). The hypothesis of uniaxial constraints is verified at convergence. It is recommended to use and update the tangent matrix quite often (every one to three iterations) in Newton’s method (MATRICE = “TANGENTE”, REAC_ITER = 1 to 3).

3.4. Keyword GEOM_FIBRE#

◊ GEOM_FIBRE =fiber

This keyword allows you to specify the name of the concept grouping the fiber groups from DEFI_GEOM_FIBRE.

3.5. Keyword MATER_SECT#

◊ MATER_SECT =subdue

Definition of the material that has the homogenized elastic characteristics of the section (therefore under the keyword ELAS), used for the calculation:

  • torsional stiffness.

  • amortization.

  • thermal expansion (ALPHA).

  • calculation of DEGE_ELNO (Eet NU).