4. Keyword ECHEC#

This repeatable factor keyword makes it possible to manage the list of moments in case of convergence failure. Each occurrence of the ECHEC keyword defines a cause of failure (see § Defining the causes of failure) and an action to be taken if this cause is satisfied (see § Define actions to be performed in case of failure). The actions may be different between each occurrence of the ECHEC keyword.

If several causes of failure are satisfied simultaneously, the order in which these failures are triggered is predetermined:

“ERREUR” takes priority over “DELTA_GRANDEUR”

4.1. Defining the causes of failure#

The EVENEMENT operand allows you to define the causes of failure.

4.1.1. Event “ERREUR”#

By default, the cause of failure is ERREUR. This case includes the following reasons:

Exceeded the maximum allowed number of Newton iterations.
Failure to integrate the law of behavior locally. The local parameters of the algorithm used for integrating the law of behavior can be found in [U4.51.11].
Deborst algorithm failed for plane constraints or 1D models. More details can be found in [U4.51.11].
Failure to solve the driving equation (see [U4.51.03]).
Failed to resolve the discreet contact issue (see [R5.03.50]). Failure occurs when the maximum number of contact iterations is exceeded or when the contact matrix is singular.
The matrix of the system is singular. Singularity detection is based on the NPREC parameter of the SOLVEUR factor keyword (see [U4.50.01]).
The iterative linear solver has reached the maximum number of Krylov iterations set by NMAX_ITER in the SOLVEUR factor keyword (see [U4.50.01]).
At convergence, physical criteria are not met when integrating the law of behavior (« event-driven » concept).

Even if no occurrence of ECHEC/EVENEMENT = “ERREUR” is found, the code automatically adds one with the default parameters (i.e. the “DECOUPE” action in “MANUEL” mode with SUBD_NIVEAU =4).

4.1.2. Event “DIVE_RESI”#

The choice of the “DIVE_RESI” event allows you to specify another possible cause of failure (« event-driven »). Failure will occur if the residue does not decrease sufficiently during Newton iterations. More precisely, there will be failure if: \(min[R(i), R(i-1)] > R(i-2)\) for \(i \ge 3\), where \(R(j)\) is the residue (RESI_GLOB_MAXI) at Newton’s iteration \(j\). If there is a failure, then the time step is undercut. The advantage of this feature is that it is not necessary to wait until we reach the end of the authorized Newton iterations to re-cut the time step in case of « notable » non-convergence. Non-convergence is realized more quickly, so time savings are expected.

note: Activating this feature with discrete contact is not recommended because in this type of calculation the residue does not generally decrease monotonically.

4.1.3. Event “DELTA_GRANDEUR”#

The choice of the “DELTA_GRANDEUR” event allows you to specify another possible cause of failure (« event-driven »). A failure will occur if the increment of a component of a field exceeds a fixed threshold, at convergence. It is then necessary to define the name of the field by the operand NOM_CHAM (field for displacement, constraints or internal variables), the name of the component by the operand NOM_CMP and the value of the reference threshold by the operand VALE_REF.

More precisely, let \(v\) be the NOM_CMP component of the field NOM_CHAM and \(valref\) be the reference value VALE_REF.

If field NOM_CHAM is a node field and \({N}_{no}\) is the set of all the nodes in the mesh, then there will be failure if at convergence:

\[max (\ Delta === {v} ^ {i} ===,\ forall i\ in {N} _ {no}) > valref\]

If field NOM_CHAM is a field at Gauss points, \({N}_{sp,pg,el}\) is the set of all the subpoints of all the Gauss points of all the elements of the model, then there will be failure if at convergence:

\[max (\ Delta === {v} ^ {i},\ forall i\ in {N} _ {sp, pg, el}) > valref\]

Increment \(\Delta\) is to be taken in the sense of increment between two moments. By default, the maximum is taken for the entire field. However, you can filter the position using the keywords GROUP_MA (for fields SIEF_ELGA and VARI_ELGA) or GROUP_NO (for field DEPL). In this case, the maximum is taken respectively from the list of groups of meshes or the list of groups of nodes.

Example 1 with law VMIS_ISOT_LINE:

ECHEC = (
    _F (
        EVENEMENT =" DELTA_GRANDEUR ",
        VALE_REF =0.1e-2,
        NOM_CHAM =" VARI_ELGA ",
        NOM_CMP ="V1",
    ),
)

Failure will occur if the cumulative plasticity increment between two time steps exceeds 0.1%.

Example 2:

ECHEC = (
    _F (
        EVENEMENT =" DELTA_GRANDEUR ",
        VALE_REF =5.0e-2,
        NOM_CHAM =" DEPL ",
        NOM_CMP ="DX",
    ),
    _F (EVENEMENT =" DELTA_GRANDEUR ", VALE_REF =5.0e-2, =5.0e-2, NOM_CHAM =" DEPL ", NOM_CMP ="DY"),
)

We will have failed if the norm (norm sup) of the movement (in 2D) varies by more than 5e-2 between two time steps.

note: In the previous two examples, although EVENEMENT =” ERREUR “is not present, it will still be enabled by default.

4.1.4. Event “COLLISION”#

This event makes it possible to break up the time step if the contact is detected (impact). This is a particularly useful feature in dynamics. Indeed, in this case, an inadequate temporal discretization will cause untimely oscillations in movement and speed at the time of the shock. To minimize these digital artifacts, it is generally recommended to finely cut the time step at the time of the collision, which is only possible for specific cases where this instant is detectable a priori by the user. In general, you can use this feature so that the cutting is done automatically.

4.1.5. Event “INTERPENETRATION”#

This event detects the interpenetration of a node into a surface when unilateral contact of the regularized type (penalization) is activated. The user gives a value of the maximum penetration that he wants to obtain (parameter PENE_MAXI) and the code then adapts the penalty coefficient (ACTION =” ADAPT_COEF_PENA “) or stops (ACTION =” ARRET”) to respect this constraint. This feature is only available for the contact in FORMULATION =” DISCRETE “(see DEFI_CONTACT [U4.44.11]).

4.1.6. Event “INSTABILITE”#

This event makes it possible to manage the progress of a non-linear calculation when instability is detected during the call to CRIT_STAB (cf. [U4.51.03] and [U4.53.01]). If this CRIT_STAB keyword is not used then this event cannot occur.

If an instability is detected, an action will then be triggered, according to two possibilities:

ACTION =” CONTINUE “: this is the default value and we will continue the calculation, even in case of instability,
ACTION =” ARRET “: if an instability is detected, then we will stop the non-linear resolution properly.

More details on the instability criterion and its use are given in the [R7.05.01] and [U2.08.04] documentation.

4.1.7. Event “RESI_MAXI”#

This event prevents the equilibrium residue from « exploding ». In fact, in certain situations, integrating the law of behavior over too long time steps increases the balance residue. It is then generally no longer possible for the residue to decrease afterwards, which leads to the failure of the calculation. By activating this event, we set a maximum value to RESI_GLOB_MAXI during Newton iterations, which makes it possible to cut the time step or to stop the calculation.

4.2. Define actions to be performed in case of failure#

Depending on the event, only certain actions are possible, see table below:

ACTION EVENEMENT	ARRET	DECOUPE	ITER_SUPPL		AUTRE_PILOTAGE	ADAPT_COEF_PENA	CONTINUE
ERREUR	OUI	OUI	OUI	OUI
DIVE_RESI		OUI
DELTA_GRANDEUR	OUI	OUI
COLLISION	OUI	OUI
INTERPENETRATION	OUI					OUI
INSTABILITE	OUI					OUI
RESI_MAXI	OUI	OUI

For example, in the most general case (EVENEMENT =” ERREUR “), there are these possibilities:

Cut out the time step (ACTION =” DECOUPE “);
Allow additional Newton iterations (ACTION =” ITER_SUPPL “);
Change the solution resulting from the pilot (ACTION =” AUTRE_PILOTAGE “);
Stop (ACTION =” ARRET “).

4.2.1. Action “ARRET”#

If you choose ACTION = “ARRET”, the calculation stops properly.

4.2.2. Action “DECOUPE”#

This action consists in redoing the time step by cutting it up. There are two methods for cutting the time step: the AUTO mode and the MANUEL mode.

4.2.2.1. Cutting in MANUEL mode#

In MANUEL mode, the time step is divided evenly. It is therefore necessary to specify the number of cuts using the keyword SUBD_PAS.

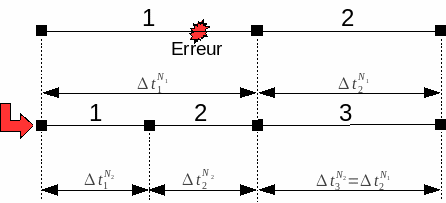
_images/Cadre3.gif — Fig. 4.1 Cut in MANUEL mode with SUBD_PAS =2#

An example is shown in the figure. Event ERREUR is triggered during time step 1, which is initially \(\Delta {t}_{1}^{{N}_{1}}\) in length. This step is then divided into two steps (SUBD_PAS = 2) of equal lengths such as \(\Delta {t}_{1}^{{N}_{2}} = \Delta {t}_{2}^{{N}_{2}} = \frac{\Delta {t}_{1}^{{N}_{1}}}{2}\). The next step (number 2 in the initial configuration) then becomes step 3, its length remains unchanged \(\Delta {t}_{3}^{{N}_{2}} = \Delta {t}_{2}^{{N}_{1}}\).

Not	1	2	3
Initial — 1	\(\Delta {t}_{1}^{{N}_{1}}\)	\(\Delta {t}_{2}^{{N}_{1}}\)
Cut — 2	\(\Delta {t}_{1}^{{N}_{2}}\)	\(\Delta {t}_{2}^{{N}_{2}}\)	\(\Delta {t}_{3}^{{N}_{2}}\)

4.2.2.2. The concept of cutting level#

The cutting of the time step is recursive: if the ERREUR event is triggered during a step that is already cut, we cut again. An example is shown in the following figure.

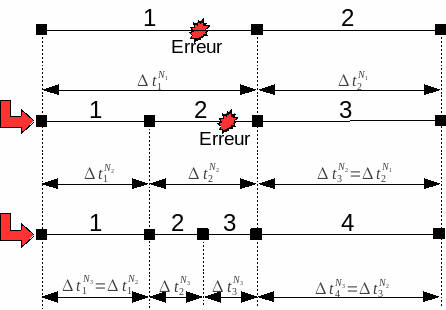
_images/Cadre1.gif — Fig. 4.2 Recursive cutting in MANUEL mode with SUBD_PAS =2#

After the first cut, the failure occurs in the (new) second time step. We recut this one with \(\Delta {t}_{2}^{{N}_{3}} = \Delta {t}_{3}^{{N}_{3}} = \frac{\Delta {t}_{2}^{{N}_{2}}}{2}\). The next time step remains unchanged \(\Delta {t}_{4}^{{N}_{3}} = \Delta {t}_{3}^{{N}_{2}}\), the first time step is converged and therefore remains unchanged \(\Delta {t}_{1}^{{N}_{3}} = \Delta {t}_{1}^{{N}_{2}}\) as well. This results in:

Not	1	2	2	3	4
Initial — 1	\(\Delta {t}_{1}^{{N}_{1}}\)	\(\Delta {t}_{2}^{{N}_{1}}\)
Cut — 2	\(\Delta {t}_{1}^{{N}_{2}}\)		\(\Delta {t}_{2}^{{N}_{2}}\)	\(\Delta {t}_{3}^{{N}_{2}}\)
Cut — 3	\(\Delta {t}_{1}^{{N}_{3}}\)		\(\Delta {t}_{2}^{{N}_{3}}\)	\(\Delta {t}_{3}^{{N}_{3}}\)	\(\Delta {t}_{4}^{{N}_{3}}\)

There cannot be a difference of more than one level between two time steps.

4.2.2.3. Cutting in AUTO mode#

The automatic cutting mode uses two possibilities:

If the triggering event is a collision (EVENEMENT =” COLLISION “), then the time step is divided with the aim of having a time step of length SUBD_INST, maintained for the duration SUBD_DUREE. If the cutting moment is too close to the collision (contact is too « grazing »), the cutting will not be effective, it is then necessary to change the initial discretization or the parameter SUBD_INSTsi (the contact becomes razor after cutting);
Otherwise, a linear extrapolation of the value of the residues is attempted.

If we write \(iter\) the Newton iteration and \({resi}^{\text{ext}}\) the value of the extrapolated residue (RESI_GLOB_RELA and/or RESI_GLOB_MAXI), then we look for \({a}_{1}\), \({a}_{2}\) and \(b\) such as:

(4.1)#\[ {resi} ^ {\ text {ext}} =\ frac {({a} _ {1}\ cdot iter + {a} _ {2})} {2})} {b}\]

Here is the algorithm used:

For \(iter = deb,fin\)

\(xx = log({resi}_{iter+1})\)

If \(iter > fin -3\)

\(poids = 2\)

Sinon

\(poids = 1\)

We calculate

\(xn = xn+poids\)

\(sx = sx+poids.xx\)

\(sy = sy+poids.iter\)

\(sxx = sxx+poids.({xx}^{2})\)

\(syx = syx+poids.xx.iter\)

End For

\({a}_{1} = sxx.sy–sx.syx\)

\({a}_{2} = -(sx.sy)+syx.xn\)

\(b = -{sx}^{2}+sxx.xn\)

To do this extrapolation, we require at least three Newton iterations and we consider that the last two iterations have twice as much weight as the first ones, if this is not possible (or if the extrapolation fails for another reason), we automatically switch to cutting mode MANUEL (SUBD_PAS =4).

4.2.2.4. Cutting control#

If the convergence is difficult and the event is triggered several times in a row, causing the time step to be divided recursively, you can stop the process in two ways in MANUEL mode:

The cutting will stop as soon as the cutting is done more than SUBD_NIVEAU times.
The cutting will stop as soon as the time step is less than SUBD_PAS_MINI.

In AUTO mode, only the SUBD_PAS_MINI keyword is available.

Note concerning the buckling calculation: When calculating elastoplastic buckling, it may happen that the tangent matrix of the system is singular during Newton iterations. By re-cutting the time step, we can get past these hard points.
Special features of operand SUBD_NIVEAU: The SUBD_NIVEAU operand is a concept that should be global to all occurrences of the ECHEC keyword. Therefore, this operand should only be defined once. In practice, this is not the case and nothing prevents setting a different value of SUBD_NIVEAU each time the ECHEC keyword occurs. To avoid this case, the algorithm will ultimately use as the global and unique value of SUBD_NIVEAU the maximum of SUBD_NIVEAU defined by the user.

4.2.3. Action “AUTRE_PILOTAGE”#

The “AUTRE_PILOTAGE” action allows you to define an action in a calculation that involves load control. When piloting, you may have to choose between two solutions (see documentation [R5.03.80]) that are often discriminated against using a RESIDU criterion.

If the user selects the “AUTRE_PILOTAGE” action and the convergence fails with the choice of solution that minimizes the residue, the current time step is repeated, after having reset it correctly, but without subdividing. At the first iteration where the choice is presented, the maximum residue solution will be chosen during this second attempt. Only subdivide if both attempts failed.

This action will therefore only be taken if the maximum number of Newton iterations is reached and if this is the first attempt.

4.2.4. Action “ITER_SUPPL”#

The “ITER_SUPPL” action allows Newton iterations to be done beyond the maximum given by ITER_GLOB_MAXI (or ITER_GLOB_ELAS). It prevents the calculation from failing for a few Newton iterations. For this, thanks to the linear extrapolation of the residues (see Action “DECOUPE”), it is possible to estimate the number of iterations of Newton necessary for convergence.

The number of iterations further is limited by the PCENT_ITER_PLUS keyword. If the estimated number of iterations is greater than The number of additional iterations is limited by the PCENT_ITER_PLUS keyword. \(\times\) ITER_GLOB_MAXI (or ITER_GLOB_ELAS), so you consider yourself to have failed. Likewise if the extrapolation is not successful. In these two cases, it is possible to activate the time step cutting (keyword SUBD_METHODE).

4.2.5. Action “ADAPT_COEF_PENA”#

If event INTERPENETRATION is triggered, this action consists in automatically increasing the value of the penalty coefficient (see operator DEFI_CONTACT [U4.44.11]) in order to reduce this interpenetration. The parameter COEF_MAXI makes it possible to specify the maximum value taken by the penalty coefficient when the automatic adaptation mechanism is used, in order to avoid matrix conditioning problems (see the precautions for using penalized methods in [U2.04.04]).

Currently, the mechanism only increases this coefficient and never decreases it, even if interpenetration no longer appears after adaptation, it therefore has a tendency to transform a problem of contact with interpenetration into a problem without contact. It is therefore appropriate to choose an initial penalty coefficient that is lower than necessary (see operator DEFI_CONTACT [U4.44.11]).

4.2.6. Action “CONTINUE”#

If event INSTABILITE is triggered, this action consists in trying to continue with the non-linear calculation. This is the default value for this event, which is the only one that can be combined with this action.