3. Examples#
3.1. Geometry and meshing GMSH#
We create a very simple geometry: a square with side \(1\). Here, we create the points, the lines, the surface; we could also have done it by translation/extrusion…
NOTE:
We create a « physical » that contains the square area of number 107.
L=1;
d=0.45;
Point (1) = {0, 0, 0, d};
Dot (2) = {L, 0, 0, d};
Dot (3) = {L, L, 0, d};
Dot (4) = {0, L, 0, d};
Line (1) = {1, 2};
Line (2) = {2, 3};
Line (3) = {3, 4};
Line (4) = {4, 1};
Line Loop (106) = {2, 3, 4, 1};
Plane Surface (6) = {106};
Physical Surface (107) = {6};
The mesh created with the 2D anisotropic algorithm is:
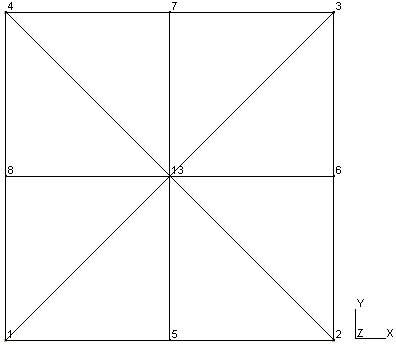
The GMSH mesh file contains the description of the nodes and meshes:
$ NOD
9
1 0 0 0
2 1 0 0
3 1 1 0
4 0 1 0
5 0.4999999999999931 0 0
6 1 0.4999999999999931 0
7 0.500000000000007 1 0
8 0 0.500000000000007 0
13 0.5000000000000001 0.5 0
$ ENDNOD
$ ELM
8
1 2 107 6 3 13 1 5
2 2 107 6 3 8 1 13
3 2 107 6 3 5 2 13
4 2 107 6 3 13 2 6
5 2 107 6 3 6 3 13
6 2 107 6 3 3 13 3 7
7 2 107 6 3 7 4 13
8 2 107 6 3 13 4 8
$ ENDELM
The syntax for this file is described in the « File Formats/GMSH mesh file format « section of the GMSH manual.
3.2. Aster mesh file produced by operator PRE_GMSH#
TITRE
AUTEUR = INTERFACE_GMSH DATE =17/07/2003
FINSF
%
COOR_3D NBOBJ =9
% FORMAT =( 1*NOM_DE_NOEUD ,3* COORD)
N1 0.00000000000000E+00 0.00000000000000E+00 0.00000000000000E+00
N2 1.00000000000000E+00 0.00000000000000E+00 0.00000000000000E+00
N3 1.00000000000000E+00 1.00000000000000E+00 0.00000000000000E+00
N4 0.00000000000000E+00 1.00000000000000E+00 0.00000000000000E+00
N5 4.99999999999993E-01 0.00000000000000E+00 0.00000000000000E+00
N6 1.00000000000000E+00 4.99999999999993E-01 0.00000000000000E+00
N7 5.00000000000007E-01 1.00000000000000E+00 0.00000000000000E+00
N8 0.00000000000000E+00 5.00000000000007E-01 0.00000000000000E+00
N13 5.00000000000000E-01 5.00000000000000E-01 0.00000000000000E+00 E+00
FINSF
%
TRIA3 NOM = INDEFINI NBOBJ =8
M1 N13 N1 N5
M2 N8 N1 N13
M3 N5 N2 N13
M4 N13 N2 N6
M5 N6 N3 N13
M6 N13 N3 N7
M7 N7 N4 N13
M8 N13 N4 N8
FINSF
%
GROUP_MA NOM = GM107
M1 M2 M3 M4 M5 M5 M6 M7 M8
FINSF
%
FIN
The eight triangles that make up the mesh square are then accessible in Aster in mesh group GM107.