2. Model formulation

Model CSSM is based on the association of behavioral equations similar to the modified Cam-Clay and Iwan models. These are detailed respectively in the [r7.01.38] and [r7.01.48] documentation.

A rheological description of model CSSM consists in superimposing these two previous models as two components, the choice being:

• A parallel association of deviatoric behavior.

• A serial association of volume behavior.

These associations are very schematically represented on Fig. 2.1.

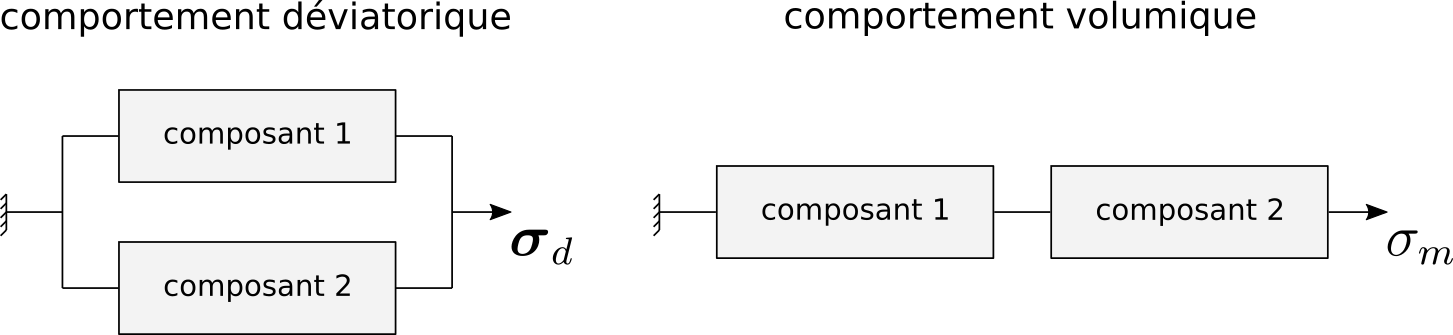
Fig. 2.1 Rheological representation of components put in parallel (deviatoric behavior) and in series (volume behavior). Components 1 and 2 see the same mean constraint \(\sigma_m\) but not the same deviator from constraints \(\boldsymbol{\sigma}_d\).

2.1. Energy and state laws

The state variables in model CSSM are the tensor of total deformations \(\boldsymbol{\varepsilon}\) and a collection of own internal variables to its two components:

• For the first component: three internal variables, tensor and scalar respectively, noted \(\boldsymbol{\varepsilon}^p,\xi\) and \(\gamma\).

• For the second component: \(N\) tensor internal variables, noted \(\left(\boldsymbol{\alpha}^i\right)_{1\leq i\leq N}\).

The free energy potential \(\psi\) is defined as follows:

\[\]

psi (boldsymbol {varepsilon},boldsymbol {varepsilon} ^p,boldsymbol {alpha} ^1,dots,boldsymbol {alpha} ^N,alpha} ^N,alpha} ^N,xi,^N,N,xi,gamma) =psi_ {varepsilon} ^p) =psi_ {e, v}left (varepsilon_v-varepsilon_v^p-sum_ {i=1} ^Nalpha^i_vright) +left [rhopsi_ {e, d} (boldsymbol {varepsilon} _d-d-boldsymbol {varepsilon} _d^p)

• (1-rho)psi_ {e, d}left (boldsymbol {varepsilon} _d-sum_ {i=1} ^Nboldsymbol {alpha} ^i_dright)right)right)right)right)right]right] +psi_ {h,1} (boldsymbol {gamma) +psi_ {h,2} (boldsymbol {right)right)right]right] +psi_ {h,1} (boldsymbol {gamma) alpha} ^1,dots,boldsymbol {alpha} ^N)

label:

free_energy

In this potential, we note that:

• The first term \(\psi_{e,v}\) takes the place of elastic energy by volume.

The second term, in square brackets, represents the elastic shear energy, which is weighted between components 1 and 2, :math:`rhopsi_{e,d}` and :math:`(1-rho)psi_{e,d}`, in*proporata of a coefficient \(\rho\). * The last two terms \(\psi_{h,1}\) and \(\psi_{h,2}\) are the energies stored by work hardening.

The following sections specify the expressions for functions \(\psi_{e,v},\psi_{e,d},\psi_{h,1}\) and \(\psi_{h,2}\).

2.1.1. Elastic energy

The elastic volume and shear energies are quadratic:

\[\]

psi_ {e, v} (x) =frac {K} {2} x^2,quadpsi_ {e, d} (boldsymbol {x}) =muboldsymbol {x}) =muboldsymbol {x}) =muboldsymbol {x})

label:

elastic_energy

\(K\) is the compression modulus and \(\mu\) is the shear modulus.

2.1.2. Energy stored by working the first component

The energy stored by work hardening \(\psi_{h,1}\), controlled by the work hardening variables \(\xi\) and \(\gamma\), is defined as:

\[\]

psi_ {h,1} (xi,gamma) = p_ {c0}left (frac {expleft (-betaxiright) -1} {beta} +etafrac {frac {frac {frac {expleft (-omegagammaright) -1} {omega}right)

label:

energie_ecrouissage_1

The parameters \(\beta\) (plastic incompressibility index) and \(p_{c0}\) (initial critical pressure) are those invoked in the expression of the critical pressure of the modified Cam-Clay model [r7.01.48].

The indices \(\eta\) and \(\omega\), which relate to work hardening controlled by the variable \(\gamma\), in particular have the effect of modulating the responses of the model during isotropic compression loads. This is illustrated in Section 5.

2.1.3. Energy stored by working the second component

The energy stored by work hardening \(\psi_{h,2}\), driven by the work hardening variables \(\left(\boldsymbol{\alpha}^i\right)_{1\leq i\leq N}\), is defined as:

\[\]

psi_ {h,2} (boldsymbol {alpha} ^1,dots,boldsymbol {alpha} ^N) =sum_ {i=1} ^Nleft (frac {h^i_D} {2}frac {H^i_D} {2} {2}boldsymbol {alpha} ^i_v} ^i_ d:boldsymbol {alpha} ^i_d+frac {H^i_D} {2}frac {H^i_D} {2}} (alpha^i_v) ^2right)

label:

energie_ecrouissage_2

where \(H_d^i\) and \(H_v^i\) are respectively the deviatoric and volume kinematic work hardening modules associated with \(\boldsymbol{\alpha}^i\).

2.1.4. State laws

Having established the expression of energy potential via its components, we can write the intrinsic dissipation volume density \(D\) as:

\[D=\ boldsymbol {\ sigma}:\ dot {\ boldsymbol {\ boldsymbol {\ varepsilon}} -\ dot {\ psi} =\ boldsymbol {X}:\ dot {\ boldsymbol {\ boldsymbol {\ varepsilon}} ^p+ \ boldsymbol {A} ^ i:\dot {\ boldsymbol {\ alpha}} ^i+p_c\ dot {\ xi} +S\ dot {\ gamma} :label: intrinsic_dissipation\]

by defining the stress tensor \(\boldsymbol{\sigma}\) and the irreversible forces \(\boldsymbol{X},\boldsymbol{A}^i,p_c\) and \(S\) combined with the internal variables by state laws:

\[\]

boldsymbol {sigma} =frac {partialpsi} {partialpartialboldsymbol {varepsilon}},quadboldsymbol {X} =-frac {partialpsi} {partialpsi} {partialpartialpsi} {partialboldsymbol {varepsilon} ^p} =-frac {partialpsi} {partialpsi} {partialpsi} {partialpsi} {partialpsi} {partialpsi} {partialpsi} {partialpsi} {partialpsi} {partialpsi}

boldsymbol {A} ^i =-frac {frac {partialpsi} {partialboldsymbol {alpha} ^i},quad p_c = -frac {partialpsi} {partialxi},quad S =-frac {partialpsi} {partialgamma} :label: law_state_1

These laws can be specified from energie_libre, energie_elastique,, energie_ecrouissage_1, and energie_ecrouissage_2:

\[\]

begin {align}

boldsymbol {sigma} &= Kleft (varepsilon_v-varepsilon_v-v^p-sum_ {j=1} ^Nalpha^j_vright)boldsymbol {I} + 2muleft (muleft (boldsymbol {varepsilon} _d-boldsymbol {I}} + 2muleft (rholeft (boldsymbol {varepsilon} _d-boldsymbol {varepsilon} _d^pright) + (1-rho) + (1-rho)left (boldsymbol {varepsilon} _d-sum_ {j=1} ^Nboldsymbol {alpha} {alpha}} ^j_dright)right)vphantom {Big {(}}\ boldsymbol {X} &= Kleft (varepsilon_v-varepsilon_v^p-sum_ {j=1} ^Nalpha^j_vright)boldsymbol {I} + 2murholeft (boldsymbol {varepsilon} _d-boldsymbol {varepsilon} _d-boldsymbol {I} + 2murholeft (boldsymbol {varepsilon} _d-boldsymbol {varepsilon} on} _d^pright)vphantom {Big {(}}\ boldsymbol {A} ^i &= Kleft (varepsilon_v-varepsilon_v-v^p-sum_ {j=1} ^Nalpha^j_vright)boldsymbol {I} + 2boldsymbol {I} + 2mu (1-rho)left (boldsymbol {varepsilon} _d-sum_ {j=1} ^Nboldsymbol {alpha} ^j_dright) -H_d^iboldsymbol {alpha} ^i_d-h_v^ialpha^i_vboldsymbol {I}boldsymbol {I}vphantom {big {(}}\ p_c &= p_ {c0}expleft (-betaxiright)vphantom {big {(}}}\ S &=eta p_ {c0}expleft (-omegagammaright)vphantom {Big {(}}} end {align}

label:

law_state_2

Note:

For convenience in solving behavior equations with MFront in Section 4, we will advantageously write the first three state laws lois_etat_2 -1, lois_etat_2 -2 and lois_etat_2 -3 in the form:

where two elastic deformations, \(\boldsymbol{\varepsilon}^e\) and \(\boldsymbol{\varepsilon}^x\), are introduced, respectively in bijection to \(\boldsymbol{\sigma}\) and \(\boldsymbol{X}\). These are easily expressed as a function of the tensor of the total deformations and the internal variables by the relationships:

2.2. Laws of evolution

The laws of evolution are deduced from the plasticity criteria specific to the two components of model CSSM defined below.

2.2.1. Plasticity criterion and flow rule for the first component

The expression for the plasticity criterion is the equation of an ellipse in plane \((X_m,X_{eq})\):

\[f (\ boldsymbol {X}, p_c, S;\ xi) =\ sqrt {\ left (\ frac {X_ {eq}} {M}\ right) ^2 +\ left (X_M+P_C-S\ right) ^2} +S-R (\ xi),\ quad\ text {with}\ quad R (\ xi) = p_ {c0}\ exp (-\ beta\ xi) :label: crite_plasticity_1\]

The parameter \(M\), called the critical state slope, has the same interpretation as in the modified Cam-Clay model [r7.01.48]. Geometrically, \(p_c-S\) positions the center of the ellipse along the hydrostatic axis, and \(S-R(\xi)\) specifies its size.

Note:

Following the expression of plasticity criterion critere_plasticite_1, it should be noted that \(p_c\) plays the role of hydrostatic restoring force. Its variation therefore predicts kinematic work hardening along the hydrostatic axis. In addition, the plasticity criterion is parameterized, as specified in the notation \(f( ; \xi)\), via the \(R(\xi)\) function. Its evolution therefore leads to the prediction of work hardening. isotropic type. Thus, as for the modified Cam-Clay model [r7.01.48], the first component of model CSSM has a combined kinematic-isotropic work hardening controlled by \(\xi\). To this work hardening is added that controlled by the variable of work hardening \(\gamma\) due to the intervention of its combined force \(S\) in the plasticity criterion critere_plasticite_1.

The initial reversibility domain associated with plasticity criterion critere_plasticite_1 is explained using state laws lois_etat_2 by:

\[f_ {0} =\ sqrt {\ left (\ frac {\ rho\ sigma_ {eq}} {M}\ right) ^2 +\ left (\ sigma_m+p_ {c0} (1-\ c0} (1-\ eta}) (1-\ eta)\ right) ^2} -p_ {c0} (1-\ eta) :label: crite_plasticite_1_initial\]

When \(\rho=0\), the initial plasticity criterion therefore no longer depends on the equivalent von Mises stress \(\sigma_{eq}\). However, regardless of the value of \(\rho\), The isotropic tension limit is zero, and is \(2p_{c0}(1-\eta)\) in isotropic compression. The Fig. 2.2 represents the effect of \(\eta\) on the initial reversibility domain. The closer this one approaches one, the more the size of the domain tends to zero by homothetic reduction around from the origin.

Fig. 2.2 Reversibility domains defined by plasticity criterion critere_plasticite_1_initial for three values of \(\eta\).

The evolution of the three internal variables \(\boldsymbol{\varepsilon}^p,\xi\) and \(\gamma\) respects the rule of normality to the plasticity criterion critere_plasticite_1:

\[\]

begin {align}

dot {boldsymbol {varepsilon}}} ^p &=dot {lambda}frac {partial f} {partialboldsymbol {X}} =dot {lambda}frac}frac {cfrac {3} {3} {2M^2}frac {3} {2M^2}boldsymbol {X} _d +left (x_m+p_c-sright)cfrac {boldsymbol {I}} {3}} {3}} {sqrt {left (cfrac {X_ {eq}} {M}right) ^2 +left (X_m+p_c-sright) ^2}}\ dot {xi} &=dot {lambda}frac {partial f} {partial p_c} =dot {lambda}frac {x_m+p_c-s} {sqrt {lambda}}frac {lambda}left {left (cfrac {partial f}} {partial p_c}} =dot {lambda}}frac {x_m+p_c-s} {left (cfrac {X_ {eq}}} {M}right) ^2 +left (x_m+p_c-sright) ^2 +left (x_m+p_c-sright) ^2 +left (x_m+p_c-sright) ^2 2}}\ dot {gamma} &=dot {lambda}frac {partial f} {partial S} =dot {lambda} -dot {lambda}frac {x_M+p_c-s} {sqrt {p_c-s} {frac {partial f}} {partial S} =dot {lambda} -dot {lambda}}frac {x_M+P_c-s} {frac {X_M+P_c-s} {left} {sqrt {partial f} {left (cfrac {X_ {eq}}} {M}right) ^2 +left (X_M+P_C-S} {left C-sright) ^2}} end {align} :label: flow_normal_1

where \(\dot{\lambda}\) is the plastic multiplier satisfying the following consistency condition:

\[\]

dot {lambda}geq 0,quad fleq 0,quaddot {lambda} f=0

label:

condition_coherence_1

So as a result of ecoulement_normal_1, we get the relationships:

\[\]

dot {xi} =dot {varepsilon} _v^p,quaddot {gamma} =dot {lambda} -dot {varepsilon} _v^p,quaddot {varepsilon} _v^p,quaddot {varepsilon} _v^p,quaddot {lambda} =sqrt {lambda} =sqrt {gamma} =sqrt {varepsilon} _v^p) ^2+ (Mdot {varepsilon} _v^p) ^2+ (Mdot {varepsilon} _v^p) ^2+ (Mdot {varepsilon} _v^p) ^2+ psilon} _ {eq} ^p) ^2}

label:

flowment_normal_1_2

The first work-hardening variable \(\xi\) is volume plastic deformation. The second \(\gamma\) is the difference between the cumulative plastic deformation \(\lambda\) and the volume one. Since ecoulement_normal_1_2 shows that \(\dot{\gamma}\geq 0\), the work hardening carried out by its combined force \(S\) is monotonic decreasing and evanescent according to lois_etat_2 -5 (\(\dot{S}\leq 0\) and \(\lim_{\gamma\rightarrow\infty} S = 0\)).

2.2.2. Plasticity criterion and flow rule for the second component

The law of evolution of internal variables \(\left(\boldsymbol{\alpha}^i\right)_{1\leq i\leq N}\) comes from plasticity criteria that differ only in their size. These criteria are hemi-elliptical in planes \((A^i_m,A^i_{eq})\):

\[F_i (\ boldsymbol {A} ^i) =\ sqrt {\ left (A^i_ {eq}\ right) ^2 +\ left (\ frac {R_i} {C}\ left\ left\ langle A^i_m+c\ right\ r_M+c\ right\ rangle\ m+c\ right\ right\ right) ^2} -R_i,\ quad\ text {with}\ quad\ langle x\ rangle =\ frac {x+|x|} {2} :label: crite_plasticity_2\]

The constant \(C\) positions the transition between the ellipses and the lines of the plasticity criteria, this value being assumed to be common to the \(N\) criteria. The constants \(R_i\) are the maximum thresholds achievable by the equivalent von Mises \(A^i_{eq}\) standards. The Fig. 2.3 illustrates three of the critere_plasticite_2 criteria for increasing values \(R_1,R_2\) and \(R_3\).

Fig. 2.3 Reversibility domains defined by plasticity criteria critere_plasticite_2 for three increasing values of \(R_1,R_2\) and \(R_3\).

Note:

When \(C\rightarrow 0\), the plasticity criteria critere_plasticite_2 approach those used in the Iwan model [r7.01.38] (von Mises criteria), with in this case a cut prohibiting the traction half-space (\(A^i_m>0\)).

The initial reversibility domain associated with plasticity criteria critere_plasticite_2 is explained using state laws lois_etat_2 by:

\[F_ {1.0} =\ sqrt {\ left ((1-\ rho)\ sigma_ {eq}\ right) ^2 +\ left (\ frac {R_1} {C}\ left\ langle\ langle\ sigma_M+C\ right\ rangle\ right) ^2} -R_1 :label: crite_plasticite_2_initial\]

having assumed \(R_1\) to be the lowest value of \(R_i\). When \(\rho=1\), the initial plasticity criterion therefore no longer depends on the equivalent stress by von Mises \(\sigma_{eq}\).

By combining critere_plasticite_1_initial and critere_plasticite_2_initial, the initial elasticity domain of the CSSM model is therefore defined by intersection \(\left\{f_{0}\leq 0 \cap F_{1,0}\leq 0\right\}\).

The evolution of the internal variables \(\left(\boldsymbol{\alpha}^i\right)_{1\leq i\leq N}\) respects the rule of normality with the critere_plasticite_2 plasticity criteria:

\[\]

dot {boldsymbol {alpha}} ^i} ^i &=dot {lambda} _ifrac {partial F_i} {partialboldsymbol {A} ^i} =dot {lambda} _i _ifrac {frac {3} {2}boldsymbol {A} ^i_d +left (cfrac {R__I} {C}right) ^2leftlangle A^i_M+Crightrightranglecfrac {boldsymbol {I}} {3}} {sqrt {left (A^i_ {eq}right) ^2 +left (cfrac {R_i} {C}}leftlangle A^i_m+cright) ^2 +left (cfrac {R_i}} {C}leftlangle A^i_m+crightrangleright) ^2}}\

label:

flow_normal_2

where \(\dot{\lambda}_i\) are the plastic multipliers satisfying the following consistency conditions:

\[\]

dot {lambda} _igeq 0,quad F_ileq 0,quaddot {lambda} _if_i=0

label:

condition_coherence_2

2.3. Determination of kinematic work hardening modules and associated thresholds

In this part, we explain how to determine the modules (kinematic hardening modules \(H_d^i,H_v^i\)) and thresholds \(R_i\) can be simplified by relying on two alternative parameters: \(\gamma_{\mathrm{hyp}}\), \(n_\mathrm{hyp}\).

2.3.1. Calculation of deviatory work hardening modules and thresholds

The calculation of deviatoric work hardening modules and thresholds follows the same methodology as that presented in the documentation [r7.01.38] assuming that the following conditions are met:

• The plasticity surface of the first component is not reached (\(f<0\)).

• The volume deformations of each \(i<N\) -th mechanism of the second component are constant (\(\dot{\alpha}_v^i=0\)).

In a nutshell, the second condition is always met if the \(i<N\) -th mechanism laminates sufficiently so that \(\alpha_v^i\) can be stabilized by kinematic work hardening along the hydrostatic axis, or much more simply when \(-\sigma_m\geq C\).

The calculation of deviatoric work hardening modules and thresholds then comes down to looking at a monotonic path when loading shear at constant pressure (\(-\dot{\sigma}_m=0\)), for example in plan \((x,y)\). In this load, the relationship between deformation rates \(\dot{\varepsilon}_{xy}\) and constraint \(\dot{\sigma}_{xy}\) is written as:

\[\]

dot {varepsilon} _ {xy} =left (2rhomu +frac {1} {cfrac {1} {2 (1-rho)mu}} +sum_ {i=1} =left (2rhoxy}} =sum_ {i=1}} =sum_ {i=1}} ^Ncfrac {mu} +sum_ {i=1}} ^Ncfrac {mathbf {H} (sqrt {3} |sigma_ {xy}} |-R_i)} {H_d^i}}right) ^ {-1}dot {sigma} _ {xy}

label:

shear_calibration_1

with \(\mathbf{H}\) the unit step function. Assuming the known answer in \(N\) points \((\varepsilon^{(i)}_{xy},\sigma^{(i)}_{xy})_{1\leq i\leq N}\), we can to derive/to establish:

\[\begin{split}R_i =\ sqrt {3} |\ sigma^ {(i)} _ {xy} |,\ quad H_i^d = \ begin {cases} \ left\ langle\ left (\ cfrac {\ sigma^ {(i+1)}} _ {xy}} -\ sigma^ {(i)} _ {xy}} {\ varepsilon^ {(i+1)}} _ {(i+1)}} _ {xy}} -\ cfrac ac {1} {2 (1-\ rho)\ mu} -\ sum_ {j=1} ^ {i-1}\ cfrac {1} {H_d^j}\ right\ rangle^ {-1}\ right\ rangle^ {-1} &\ quad\ rangle^ {-1} &\ quad\ text {si}\ quad i<N\\ 0 &\ quad\ text {if}\ quad i=N \ end {cases} :label: shear_calibration_2\end{split}\]

Note then that calibration_cisaillement_2 -2 leads to \(H_d^{m}=0\Longrightarrow\left(H_d^i\right)_{m+1\leq i\leq N}=0\). \(m-1<N\) modules are therefore zero with consistently \(H_d^N=0\), which allows the model to predict a critical state in accordance with the system that we are establishing systeme_etat_critique.

The calculation of the \(H_d^i\) work hardening parameters is carried out by fixing \(N=10\) points interpolation on a logarithmic base ten scale, between \(2\varepsilon^{(1)}_{xy}=10^{-5}\) and \(2\varepsilon^{(10)}_{xy}=10^{-2}\). Points \((\varepsilon^{(i)}_{xy},\sigma^{(i)}_{xy})_{1\leq i\leq 10}\) satisfy a « modified hyperbolic » relationship, commonly used in soil dynamics, which is written as:

\[\]

mu_ {mathrm {secant}} =frac {mu}} {1+left (cfrac {2varepsilon_ {xy}} {gamma_ {mathrm {hyp}}}}} =frac {mu}}} =right) ^ {n_ {mathrm {hyp}}}}},quadtext {with}quadmu_ {mathrm {secant}} =frac {sigma_ {xy}} {2varepsilon_ {xy}}}

label:

shear_calibration_3

\(\gamma_{\mathrm{hyp}}\) and \(n_\mathrm{hyp}\) are therefore two parameters of the model CSSM to be filled in, which have an interpretation common to the work hardening parameters documented in [r7.01.38].

2.3.2. Expression of volume work hardening modules

Obtaining the \(H_v^i\) volume work hardening modules is justified by the desire to effectively integrate the evolution equations present in critere_plasticite_2 and condition_coherence_2, without requiring the resolution of a non-linear equation for plastic multipliers. In fact, it is proved that this is possible when the following condition is met:

\[H_v^i =\ frac {3} {2} {2}\ left (\ frac {C} {R_i}\ right) ^2H_d^i :label: expression_module_volume_hardening_volume\]

Under this condition, the numerical integration of model CSSM then makes it possible to reduce the number of equations to be solved. This procedure is detailed in Section 4.

2.4. Critical state equations

In this paragraph, we seek to establish the equations of model CSSM corresponding to the critical state. This state is defined by constant stresses and volume deformation, asympotically achieved in a monotonic loading. We assume that this state is reached for each of components 1 and 2 of the model.

For the first component, if the stresses remain constant, there is no more work hardening due to \(\xi\) or \(\gamma\). In this situation, it is proved that the following conditions are met:

\[X_ {eq} +M x_M=0,\ when X_M+P_C=0 :label: critical_status_1\]

Now, state laws lois_etat_2 -1 and lois_etat_2 -2 show that \(X_m=\sigma_m\). So etat_critique_1 is equivalent to:

\[X_ {eq} +M\ sigma_m=0,\ quad\ sigma_m+p_c=0 :label: critical_status_2\]

As for the second component, following calibration_cisaillement_2 -2 and expression_module_ecrouissage_volumique, \(H_d^{m}=H_v^{m}=0=0\) for a certain \(m\leq N\). So state laws lois_etat_2 -1 and lois_etat_2 -3 show that \(A^m_m=\sigma_m\). The verification of the criterion critere_plasticite_2 then leads to:

\[A^m_ {eq} = R_m\ sqrt {1-\ left\ langle\ sigma_m/C+1\ right\ rangle^2} :label: critical_status_3\]

In addition, we recall lois_etat_2 -1, lois_etat_2 -2 and lois_etat_2 -3 which establish that \(\boldsymbol{\sigma}_d=\boldsymbol{X}_d+\boldsymbol{A}^m_d\). By admitting that these last two tensors are collinear and in the same sense, equations etat_critique_2 -1 and etat_critique_3 imply that:

\[\]

sigma_ {eq} +Msigma_m=r_msqrt {1-leftlanglesigma_m/C+1rightrangle^2}

label:

critical_status_4

Finally, it is shown that the total volume deformation remains constant only if \(\sigma_m+C<0\). Otherwise, it only evolves like \(\dot{\varepsilon}_v=\dot{\alpha}_v^m>0\).

In short, it should be noted that the critical state predicted by model CSSM can be defined by the following set of equations:

\[\]

begin {align}

dot {boldsymbol {sigma}} =boldsymbol {0}\ dot {varepsilon} _v=0\ sigma_m+p_c = 0\ sigma_M+C<0\ sigma_ {eq} +Msigma_m=r_msqrt {1-leftlanglesigma_m/C+1rightrangle^2} end {align} :label: critical_status_system

Fig. 2.4 represents three systeme_etat_critique -5 critical state lines based on values of \(R_m\) in the stress meridian plane. For \(\sigma_m+C<0\), it indicates that the model CSSM predicts a dilated state (\(\dot{\varepsilon}_v=\dot{\alpha}_v^m>0\)).

Fig. 2.4 Examples of critical state lines systeme_etat_critique -5 for three values of \(R_m\) in the stress meridian plane.

2.5. Eliminating negative work hardening from the model

Model CSSM inherits the same work hardening as that of the modified Cam-Clay model, driven by the \(\xi\) variable. Now we have shown after the criterion of plasticity critere_plasticite_1 that this variable produces two workings:

• A kinematic one: this mechanism is associated with its conjugate force \(p_c\) conjugate by the state law lois_etat_2 -4, playing the role of a hydrostatic restoring force. This work hardening moves the plasticity surface into the stress meridian plane without changing its size or shape.

• The other isotropic: this mechanism is linked to the parametrization of the criterion through the function \(R(\xi)\). This work hardening changes the size of the plasticity surface.

Kinematic work hardening alone cannot produce negative work hardening, due to the convexity of the potential from which \(p_c\) drifts. On the other hand, negative isotropic work hardening can occur if \(R(\xi)\) decreases, which potentially poses numerical stability problems in a finite element calculation. To avoid this situation, it is proposed to replace function \(R(\xi)\), after discretization incremental loading times, by:

\[R_ {n+1} = R_n\ max\ max\ left\ {1,\ exp\ left (-\ beta\ Delta\ xi\ right)\ right\},\ quad\ text {with}\ quad R_0=p_ {c0},\ quad\ Delta\ xi =\ xi_ {n+1} -\ xi_n :label: suppression_softening\]

\(\left(R_n\right)_{n\geq 0}\) is a growing number. We then only take into account cumulative isotropic positive work hardening that would have been predicted by the initial function \(R(\xi)\) critere_plasticite_1 -2.

Note:

If applications of the CSSM model require an interest in predicting negative work hardening, the restriction imposed by suppression_adoucissement can, if necessary, be removed. in later developments.