3. Model description#

3.1. Clean creep#

To model the phenomenon of natural creep, the proposed model relies on simple rheological models (figure) comprising in series an elastic body (described by behavior ELAS), a linear Kelvin Voigt solid for modeling reversible creep (recovery), and a Maxwell liquid with a non-linear viscosity to model long-term creep. The spherical and deviatory chains are equivalent in their construction.

The Kelvin Voigt stage has a deformation limit managed by the elasticity module. The particularity of the model is based on the choice of the nonlinearity assigned to the viscosity of the Maxwell body.

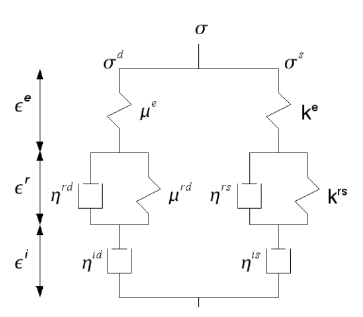
_images/100000000000016B0000013D19549509B63056EF.png

Figure 3.1-1: Rheological diagram distinguishing the spherical and deviatoric part of the stress tensor

3.1.1. Description of the spherical part#

The spherical deformation of natural creep is written as the sum of a reversible part and an irreversible part:

(3.1)#\[\begin{split} {\ mathrm {\ epsilon}} ^ {\ text {fs}}} =\ underset {\ begin {array} {c}\ text {part}\\ text {reversible}\ end {array}} {\ underset {array}} {\ underset {}} {\ underset {}}} {\ underset {}}} {\ underset {}} {\ underset {}} {\ underset {}} {{\ underset {}} {{\ mathrm {\ epsilon}}} _ {r} ^ {\ text {fs}}}}} +\ underset {\ array}}} {\ underset {}}} {\ underset {}} {\ underset {}} {\ underset {}} {{c}\ text {part}\\\ text {irreversible}\ end {array}} {\ underset {} {{\ mathrm {\ epsilon}}} _ {i}} ^ {i} ^ {\ text {fs}}}}\end{split}\]

The process of spherical creep deformation is governed by the following equations:

(3.2)#\[ h\ cdot {\ mathrm {\ sigma}}} ^ {s}} ^ {k} ^ {\ mathit {rs}}\ cdot {\ mathrm {\ epsilon}} _ {r} ^ {\ mathit {fs}}} ^ {\ mathit {fs}}} ^ {\ mathrm {\ eta}}} ^ {\ mathit {rs}}\ cdot {\ dot {\ mathrm {\ mathrm {fs}}}\ cdot {\ dot {\ mathrm {\ mathrm {fs}}} + {\ mathrm {\ fs}}} + {\ mathrm {\ eta}}} ^ {\ mathit {rs}}\ cdot {\ dot {\ mathrm {\ mathrm {fs}}} ^ {}}} _ {r} ^ {\ mathit {fs}}\]

and:

(3.3)#\[ h\ cdot {\ sigma} ^ {s} = {\ eta} ^ {\ eta} ^ {\ mathrm {is}}\ cdot {\ dot {\ epsilon}}} _ {i} ^ {\ i} ^ {\ mathrm {fs}}\]

with:

  • \({k}_{r}^{s}\) the compressibility module associated with reversible spherical natural creep,

  • \({\eta }_{r}^{s}\) the viscosity of the Kelvin Voigt stage associated with the reversible spherical proper creep,

  • \({\eta }_{i}^{s}\) the non-linear spherical viscosity of Maxwell’s fluid.

Indicator \(\dot{}\) associated with any variable describes the speed of change of that variable.

3.1.2. Description of the deviatoric part#

The deviatoric self-creep deformation is also written as the tensor sum of a reversible part and an irreversible part:

(3.4)#\[\begin{split} \ underset {\ begin {array} {c}\ text {deformation}\\ text {deformation}\\ text {deviatory}\\ text {total}\ end {array}} {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {\ underline {{contribution}\\ text {reversible}\ end {array}}} {\ underset {array}} {\ underset {} {{\ underline {\ underline {\ mathrm {\ epsilon}}}}} _ {r} ^ {\ text {fd}}}}}} +\ underset {\ text {fd}}} {\ text {fd}}} {\ text {fd}}}} {\ text {fd}}}}} +\ underset {\ begin {array}}}} {\ underset {\ begin {array}}} {underset {array}} {\ underset {array} {c}\ text {contribution}\\ text {irreversible}\ end {array}} {underline}} {\ text {epsilon}}}} {\ underset {set {} {{\ underline {\ underline {\ underline {\ mathrm {\ epsilon}}}}} _ {i} ^ {\ text {fd}}}}\end{split}\]

The*th* main component of the total deviatoric deformation is governed by the equations:

(3.5)#\[ {\ mathrm {\ eta}} _ {r} ^ {d}\ cdot {\ dot {\ mathrm {\ epsilon}}}} _ {r} ^ {\ mathit {fd}, j} + {k} + {k} _ {r} ^ {d}\ cdot {\ mathrm {\ epsilon}}} _ {r} ^ {\ mathit {fd}, j} = h\ cdot {\ mathrm {\ sigma}}} ^ {d, j}\]

And:

(3.6)#\[ {\ mathrm {\ eta}} _ {i} ^ {d}\ cdot {\ dot {\ mathrm {\ epsilon}}}} _ {i} ^ {\ mathit {fd}, j}, j} =h\ cdot {\ mathrm {\ sigma}} ^ {d, j}\]

with:

  • \({k}_{r}^{d}\) the shear modulus associated with reversible deviatoric proper creep,

  • \({\eta }_{r}^{d}\) the viscosity of the Kelvin Voigt stage associated with reversible deviatoric proper creep,

  • \({\eta }_{i}^{d}\) the nonlinear deviatory viscosity of Maxwell’s fluid.

3.1.3. Description of viscous nonlinearity#

The non-linearity of the viscosity is interpreted according to [bib6] as the result of a spherical consolidation of the sample ([bib7]) and of an entanglement or blocking of the movements of the sheets CSH, constituents of the mortar. A « consolidation » coefficient is therefore introduced according to the same idea to control the evolution of viscosities. This additional coefficient affects the laws of evolution of Maxwell bodies (spherical and deviatoric). It is directly dependent on the norm of the tensor of cumulative irreversible delayed deformations. This extension of the hypotheses posed by [bib6] allows non-linearity to be taken into account for all types of paths (with or without spherical loading). The explicit formulation of Maxwell’s bodies is as follows:

(3.7)#\[ {\ eta} _ {i} ^ {s} = {\ eta} = {\ eta} _ {i\ mathrm {,0}}} ^ {s}\ cdot\ mathrm {exp}\ left (\ frac {=== {\ epsilon} = {\ epsilon}} _ {\ epsilon} _ {\ epsilon} _ {m} _ {m} ^ {m} ^ {\ mathit {fi}}\]

with:

  • \({\eta }_{i\mathrm{,0}}^{s}\) the initial viscosity of Maxwell’s fluid relating to the spherical part

  • \({\eta }_{i\mathrm{,0}}^{d}\) the initial viscosity of Maxwell’s fluid relating to the deviatory part

  • \(\kappa\) the characteristic deformation linked to a viscosity that is amplified by a factor \(\mathrm{exp}(1)\).

  • \(∣∣{\varepsilon }_{m}^{\mathit{fi}}∣∣\) The equivalent irreversible deformation, that is to say the norm of the complete tensor (spherical and deviatoric) of irreversible creep deformations, which is the maximum value reached during loading.

The construction of \(∣∣{\epsilon }_{m}^{\mathit{fi}}∣∣\) follows the following logic: \(∣∣{\epsilon }_{m}^{\mathit{fi}}∣∣=\mathit{max}\left(∣∣{\epsilon }_{m}^{\mathit{fi}}∣∣,\sqrt{{\underline{\underline{\epsilon }}}^{\mathit{fi}}\mathrm{:}{\underline{\underline{\epsilon }}}^{\mathit{fi}}}\right)\).

3.1.4. Restricting the number of model parameters#

The equivalence of the deviatoric and spherical rheological chains makes it possible to obtain, by respecting the following expression, an apparent Poisson’s ratio of constant creep:

(3.8)#\[ \ frac {{\ eta} _ {i\ mathrm {,0}}} ^ {0}} ^ {s}} {{\ eta} _ {i\ mathrm {0}}} ^ {d}} =\ frac {{\ eta}} _ {{\ eta}} _ {{\ eta}}} =\ frac {{k}}} =\ frac {{\ eta}} _ {r}\ eta} _ {r} {\ eta} _ {r} {\ eta} _ {r}} ^ {s}}} {k} _ {r} ^ {d}} =\ frac {\ left (1+\nu\ right)} {\ left (1-2\ cdot\nu\ right)} =\ beta\]

For the use of model BETON_BURGER on uniaxial creep tests, radial deformations of the samples are rarely available, making it difficult to identify all the parameters of the model. A first approximation consists in assuming the relationship () and thus limits the number of parameters to be determined to four.

3.1.5. Thermo-activation of natural creep deformations#

The experimental results of specific creep tests at temperature show that the creep deformation is thermo-activated. For temperatures \(T\) below 55°C, it obeys an Arrhenius law:

(3.9)#\[ {\ epsilon} ^ {f} (T) = {\ epsilon} ^ {f} ({T} _ {0})\ cdot\ mathrm {exp}\ left (\ frac {- {E} _ {\ mathit {e}} _ {\ mathit {ac}} _ {T} _ {0}}\ right)\ right)\]

with:

  • \({T}_{0}\) the reference temperature

  • \({E}_{\mathit{ac}}\) activation energy

  • \(R\) the ideal gas constant (8.3144621 \({\mathit{J.K}}^{-1}\mathrm{.}{\mathit{mol}}^{-1}\))

To satisfy this relationship and while maintaining a constant characteristic time, the stiffness of the springs and the viscosity of the shock absorbers are modified in the following manner:

(3.10)#\[ {k} ^ {\ mathit {rs}} (T) = {k} ^ {k} ^ {\ mathit {rs}} ({T} _ {0})\ cdot\ mathrm {exp}\ left (\ frac {{E}} _ {\ frac}} _ {E} _ {E} _ {E} _ {E} _ {0})\ cdot\ mathrm {exp}\ left (\ frac {1} {T}\ left} -\ frac {{E}} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ T} _ {0}}\ right)\ right)\]
(3.11)#\[ {k} ^ {\ mathit {rd}} (T) = {k} ^ {k} ^ {\ mathit {rd}}} ({T} _ {0})\ cdot\ mathrm {exp}\ left (\ frac {{E}} _ {\ frac}} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} _ {E} T} _ {0}}\ right)\ right)\]
(3.12)#\[ {\ eta} ^ {\ mathit {rs}} (T) = {\ eta}} (T) = {\ eta}} ^ {\ mathit {rs}} ({T} _ {0})\ cdot\ mathrm {exp}\ left\ left\ left (\ frac {exp}\ left}\ left (\ frac {1} {T}\ left}\ left (\ frac {1} {T}}\ left (\ frac {1} {T}}\ left (\ frac {1} {T}}\ left) (\ frac {1} {T}}\ left (\ frac {1} {T}} -\ frac {1}} (T) {{T} _ {0}}\ right)\ right)\]
(3.13)#\[ {\ eta} ^ {\ mathit {rd}} (T) = {\ eta}} (T) = {\ eta}} ^ {\ mathit {rd}} ({T} _ {0})\ cdot\ mathrm {exp}\ left\ left\ left (\ frac {exp}\ left}\ left (\ frac {1} {T}\ left}\ left (\ frac {1} {T}}\ left (\ frac {1} {T}}\ left (\ frac {1} {T}}\ left) (\ frac {1} {T}} -\ frac {1}} (T) {{T} _ {0}}\ right)\ right)\]
(3.14)#\[ {\ eta} _ {0} ^ {\ mathit {is}} (T) = {\ eta}}} (T) = {\ eta} _ {is}} ({T} _ {0})\ cdot\ mathrm {exp}\ exp}\ left\ left\ left (\ frac {is}}\ left (\ frac {1}}\ left (\ frac {1}}\ left (\ frac {1} {T}}} {R}\ cdot\ left (\ frac {1}} {T}} -\ frac {1} {{T} _ {0}}\ right)\ right)\]
(3.15)#\[ {\ eta} _ {0} ^ {\ mathit {id}} (T) = {\ eta}} (T) = {\ eta} _ {id}} ({T} _ {0})\ cdot\ mathrm {exp}\ exp}\ left\ left (\ frac {{id}} _ {\ mathit {ac}}}} {R}\ cdot\ left (\ frac {exp}}\ left (\ frac {1}} {T}} -\ frac {1} {{T} _ {0}}\ right)\ right)\]
\[\]

: label: eq-21

kappa (T) =frac {kappa ({T} _ {0})} {mathrm {exp}left (frac {{E} _ {mathit {ac}}}}} {R}} {R}}cdotleft (cdotleft (frac {1} {0}}}} {R}cdotleft (frac {1} {0}}}} {R}cdotleft (frac {1} {T}} -frac {1} {T} _ {0}}}right)right)}

To determine activation energy \({E}_{\mathit{ac}}\), it is strongly recommended to use experimental temperature creep test data. Without this data, the default value for activation energy is 17.5 kJ.mol-1.

The temperature field is therefore essential prior to the mechanical calculation. If, however, the temperature field is not provided, thermo-activation is not taken into account in the model, i.e. \({k}^{\mathit{rs}}(T)={k}^{\mathit{rs}}({T}_{0})\), \({k}^{\mathit{rd}}(T)={k}^{\mathit{rd}}({T}_{0})\), \({\eta }^{\mathit{rs}}(T)={\eta }^{\mathit{rs}}({T}_{0})\), \({\eta }^{\mathit{rd}}(T)={\eta }^{\mathit{rd}}({T}_{0})\), \({\eta }_{0}^{\mathit{is}}(T)={\eta }_{0}^{\mathit{is}}({T}_{0})\),, \({\eta }_{0}^{\mathit{id}}(T)={\eta }_{0}^{\mathit{id}}({T}_{0})\), \(\kappa (T)=\kappa ({T}_{0})\).

3.2. Desiccation creep#

It is assumed to be able to break down desiccation creep \(\mathrm{\Delta }{\mathrm{\epsilon }}^{\mathit{fdess}}\) into two parts called intrinsic and structural [bib4]:

(3.16)#\[ \ mathrm {\ Delta} {\ mathrm {\ epsilon}}} ^ {\ mathit {fdess}} =\ mathrm {\ Delta} {\ mathrm {\ epsilon}}} _ {\ text {int}}} _ {\ text {int}}} _ {\ text {int}}} ^ {\ text {fdess}} ^ {\ text {fdess}} +\ mathrm {\ delta} {\ epsilon}} _ {\ text {int}}} _ {\ text {int}}} ^ {\ text {int}}} ^ {\ text {fdess}} ^ {\ text {fdess}} +\ mathrm {\ Delta} {\ epsilon}} _ {\ text {int}}} _ {\ text {int} t}} ^ {\ text {fdess}}\]

It is agreed that structural deformation is not a deformation component in itself, so in this document the only component of desiccation creep concerns the intrinsic part:

(3.17)#\[ \ mathrm {\ Delta} {\ mathrm {\ epsilon}}} ^ {\ mathit {fdess}} =\ mathrm {\ Delta} {\ mathrm {\ epsilon}}} _ {\ text {\ epsilon}}} _ {\ text {\ epsilon}}} _ {\ text {\ epsilon}}} _ {\ text {\ epsilon}} _ {\ text {\ epsilon}}} _ {\ text {\ epsilon}}} _ {\ text {\ epsilon}} _ {\]

Bazant et al. [bib10] suggest that drying and applying a compression load simultaneously are responsible for the microdiffusion of molecules between macro-pores and micro-pores. The micro-diffusion of water molecules would promote the breaking of the bonds between the gel particles inducing the deformation of desiccation creep. It is one of the most complicated physicochemical phenomena to model resulting from a coupling between stress, natural creep and drying. They propose the following equation (shock absorber equation) to take into account the (intrinsic) desiccation creep at the elementary level:

:math:`{dot{mathrm{epsilon }}}^{text{fdess}}=frac{left

dot{h}right

sigma }{{mathrm{eta }}^{mathit{fd}}}`

with:

  • \({\mathrm{\epsilon }}^{\text{fdess}}\) the deformation of the desiccation creep,

  • \({\eta }^{\mathit{fd}}\) a material parameter (in \(\left[\mathit{Pa}\cdot \mathit{sec}\right]\) in the S.I.),

  • \(h\) the relative humidity that changes over time, given the evolution problem.