3. Three-dimensional formulation of the model

The presentation of the Barcelona model in a three-dimensional formulation extends that established previously in the case of isotropic loads. To do this, we restrict ourselves here to the equations allowing the numerical integration of the model, without justifying the Barcelona model based on the thermodynamic principles applied to the modeling of unsaturated soils. The reader interested in this topic will find some elements related to these difficulties in reference ([bib3] __, [bib4] __).

3.1. Elastic behavior

Note the total strain tensor \(\boldsymbol{\varepsilon}\), the plastic strain tensor \(\boldsymbol{\varepsilon}^p\), and \(\boldsymbol{\varepsilon}^e=\boldsymbol{\varepsilon}-\boldsymbol{\varepsilon}^p\) the elastic strain tensor. The net stress tensor expression \(\boldsymbol{\sigma}''=\boldsymbol{\sigma}+p_g\boldsymbol{I}\) is written as:

\[\]

boldsymbol {sigma} » = Ktildekappaleft (

1-expleft (-frac {varepsilon^e_v} {tildekappa} -frac {tildekappa_s} {tildekappa}lnleft}lnleft (1+frac {p_c} {frac {p_c} {K_stildekappa_s} {tildekappa}}right)left (1+frac {p_c} {tildekappa_s}right) right)boldsymbol {I} +2muboldsymbol {varepsilon} ^e_d :label: constraint-expression

Note that shear elasticity is linear, where \(\mu\) is the shear modulus. The visualization of volume elasticity, which is clearly non-linear, is analyzed by differentiating and inverting expression_contrainte, leading to:

\[d\ varepsilon_v^e =-\ tilde\ kappa\ frac {dp "} {p"+k\ tilde\ kappa} -\ tilde\ kappa_s\ frac {dp_c} {p_c+k_s\ tilde\ kappa_s} :label: elasticite_incrementale_2\]

having again noted \(p''=-\sigma_m''\) the net pressure. Comparing elasticite_incrementale_1 and elasticite_incrementale_2, using equivalence_deformation_indice_des_vides_2 -a, the equality of the two expressions occurs when:

\[\]

tildekappa =frac {kappa} {1+e_0},quadtildekappa_s =frac {kappa_s} {1+e_0},quad K_stildekappa} {1+e_0},quad K_Stildekapparightarrow 0

label:

equivalence_parameters

Satisfying the first three expressions poses a priori no particular difficulty. On the other hand, you cannot strictly check the last one with \(K=0\). This impossibility comes from the fact that the incremental relationship elasticite_incrementale_1 assumes an initial state with zero volume deformation but non-zero net pressure, which is not the case in the elasticite_incrementale_2 relationship. In the present case, \(K\) acts as an initial compressibility module under net stress, since elasticite_incrementale_2 results in:

\[d\ varepsilon_v^e\ big {|} {|} _ {p"=0, dp_c=0} =-\ frac {dp "} {dp"} {K} :label: initial_compressibility_module\]

3.2. Range of elasticity

The elasticity domain of the Barcelona model is deduced from the two plasticity criteria introduced domaine_elasticite_isotrope, now taking into account the deviatoric component of the net stress tensor. These two plasticity criteria can be written as:

\[f_1 (\ boldsymbol {\ sigma}}", p_c, e_p) =\ sqrt {\ left (\ frac {\ sigma_ {eq} "} {M}\ right) ^2+\ left (\ sigma_m"+\ frac {p_ {con} (p_c, e^p) -kp_c} {2}\ right) ^2}} - \ frac {p_ {con} (p_c, e^p) +kp_c} {2},\ quad f_2 (p_c, e_p) = p_c - s_0 (e^p) :label: elasticity_domain\]

The parameter \(M\), called the critical state slope, has the same interpretation as in the modified Cam-Clay model ([r7.01.48]). A three-dimensional view of the elasticity domain is shown on Fig. 3.1 for a fixed \(e^p\) plastic void index.

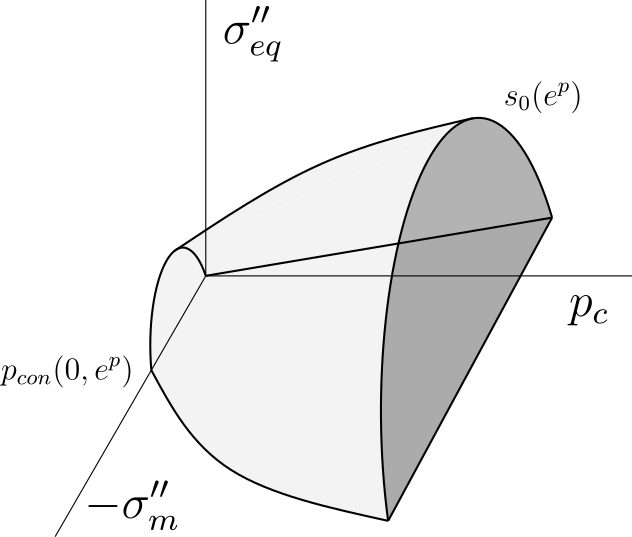
Fig. 3.1 Range of elasticity with a constant plastic void index.

note

In domaine_elasticite, the same punctuation (« , ») is used to refer to the intervention of \(\boldsymbol{\sigma}'',p_c\) and \(e_p\) in both plasticity criteria, without distinguishing the role of each as an argument or parameter. This simplified notation is accepted insofar as the Barcelona model presented here does not claim to demonstrate its thermodynamic accuracy.

3.3. Work hardening functions

The two work hardening functions, which are involved in the two plasticity criteria domaine_elasticite, take the same forms as those obtained in Section 2 taking into account the equivalence_deformation_indice_des_vides_2 -b relationship. So we write:

\[p_ {con} (p_c, e^p) =\ tilde {p} _ {con} (p_c,\ varepsilon_v^p) = p_r\ left (\ cfrac {p^0_ {con}\ exp\ left}\ exp\ left (-\ cfrac {\ varepsilon_v^p} {\ tilde {\ lambda} _0-\ tilde {\ kappa}}\ right)} {p_r}\ right) ^\ cfrac {\ tilde {\ lambda} _0-\ tilde {\ kappa}}} {\ tilde {\ lambda}} (p_c) -\ tilde {\ kappa}},\ quad s_0 (e^p) =\ tilde {s} _0 (\ varepsilon_v^p) =\ left (s_0^0+k_s\ tilde\ kappa_s\ right)\ exp\ left (-\ frac {\ varepsilon_v^p} {\ tilde\ lambda_s-\ tilde\ kappa_s\ right)\ exp\ left (-\ frac {\ varepsilon_v^p} {\ frac {\ varepsilon_v^p} {\ tilde\ lambda_s-\ tilde\ kappa_s\ right) - K_s\ tilde\ kappa_s :label: ecrouissage_expression\]

where:

\[p^0_ {con} = p_ {con} (0,0),\ quad\ tilde {\ lambda} _0=\ frac {\ lambda_0} {1+e_0},\ quad\ tilde {\ tilde {\ lambda} (p_c) =\ frac {\ lambda (p_c)} {1+e_0},\ quad s^0_0 = s_0 (0),\ quad\ tilde\ tilde\ lambda_s=\ frac {\ lambda_s} {1+e_0} :label: working_equivalence\]

3.4. Flow rules

The flow rule relating to the plastic deformation tensor rate is written using two flow potentials \(g_1\) and \(g_2\):

\[\]

dot {boldsymbol {varepsilon}}} ^p =dot {lambda} _1frac {partial g_1} {partialboldsymbol {sigma} « } »} +dot {lambda}} _2dot {lambda} _2frac {partial g_2} {partialboldsymbol {sigma} « } +dot {lambda} _2frac {partial g_2} {partialboldsymbol {sigma} »}

label:

plastic_flow

where the plastic multipliers \(\dot{\lambda}_1\) and \(\dot{\lambda}_2\) verify the consistency conditions:

\[\]

begin {align}

&dot {lambda} _1geq 0,quad f_1leq 0,quaddot {lambda} _1f_1 = 0\ &dot {lambda} _2geq 0,quad f_2leq 0,quaddot {lambda} _2f_2 = 0 end {align} :label: conditions_consistency

The two flow potentials in ecoulement_plastique are written as:

\[g_1 (\ boldsymbol {\ sigma}}", p_c, e_p) =\ sqrt {\ alpha\ left (\ frac {\ sigma_ {eq} "} {M}\ right) ^2+\ left (\ sigma_m"+\ frac {p_ {con} (p_c, e^p) -kp_c} {2}\ right) ^2} -\ frac {p_ {con} (p_c, e^p) +kp_c} {2},\ quad g_2 (\ boldsymbol {\ sigma}") = -\ sigma_m" :label: flow_potentials\]

The coefficient \(\alpha\), when taken to be different from one, is suggested to take a value that makes it possible to predict a state of oedometric deformation for a state of stress defined by the earth pressure coefficient at rest given by Jacky’s formula [bib2] __, which leads to:

\[\]

alpha =frac {M (9-M) (3-M)} {9 (6-M)}frac {lambda_0} {lambda_0-kappa}

label:

alpha_expression

3.5. Critical state equations

In this paragraph, the critical state equations of the Barcelona model are established. This state corresponds to a monotonous deformation loading for which the state of the net stresses and the volume deformation remain constant. For this, it is assumed that the capillary pressure is constant, and that only the surface of the first plasticity criterion domaine_elasticite -a is reached.

Since the volume of plastic deformation should cancel out, the direction of flow given by ecoulement_plastique and potentiels_ecoulement -a implies:

\[\]

sigma_m+frac {p_ {con} (p_c, e^p) -kp_c} {2} =0

label:

critical_state_pressure

In this situation, the expression of the first plasticity criterion domaine_elasticite -led to:

\[\]

sigma »_ {eq} = Mfrac {p_ {con} (p_c, e^p) +kp_c} {2}

label:

critical_status_equivalent_constraint

The two previous relationships allow us to conclude:

\[\]

sigma »_ {eq} + M (sigma_m » -kp_c) =0

label:

right_critical_state

Thus, in summary, the critical state predicted by the Barcelona model, with capillary pressure assumed to be constant, is defined by the following set of equations:

\[\]

begin {align}

dot {boldsymbol {sigma}} « =boldsymbol {0}\ dotvarepsilon_v=0\ sigma_m+frac {p_ {con} (p_c, e^p) -kp_c} {2} =0\ sigma »_ {eq} + M (sigma_m » -kp_c) =0 end {align} :label: critical_status_system

In particular, systeme_etat_critique -d highlights the gain in cohesion that results from a higher value of the imposed capillary pressure.