3. The continuous model#
3.1. Elastic behavior#
The elastic behavior is controlled by a linear law, with a constant module independent of the stress state. The 2 parameters characterizing this behavior are the elasticity module E and the Poisson’s ratio \(\nu\).
\(\dot{s}=2\mu (\dot{e}-\dot{{e}^{p}})\) eq 3.1-1
\(\dot{{I}_{1}}=\mathrm{3K}(\dot{{\varepsilon }_{\nu }}-\dot{{\varepsilon }_{\nu }^{p}})\) eq 3.1-2
3.2. Plasticity criterion#
The wording adopted is that of [bib2].
3.2.1. Charging surface#
3.2.1.1. Expression of the Eagle criterion in major and minor constraints#
\(f={(\frac{\sqrt{\frac{2}{3}}}{{\sigma }_{c}})}^{\frac{1}{a({\gamma }^{p})}}\left[(\mid {\sigma }_{1}-{\sigma }_{3}\mid )\frac{1}{a({\gamma }^{p})}-({\sigma }_{c})\frac{1}{a({\gamma }^{p})}(\frac{m({\gamma }^{p})}{{\sigma }_{c}}(-{\sigma }_{3})+s({\gamma }^{p}))\right]\) eq 3.2.1.1-1
3.2.1.2. General expression#
The preceding expression is transformed as a function of the first invariant and of the stress deviator, by resetting the criterion to a triaxial under compression, in order to obtain:
\(f={(\frac{g(s)}{{\sigma }_{c}{h}_{c}^{0}})}^{\frac{1}{a({\gamma }^{p})}}-u(\sigma ,{\gamma }^{p})\le 0\) eq 3.2.1.2-1
with:
\(h(\theta )={(1+{\gamma }_{\text{cjs}}\text{cos}(3\theta ))}^{1/6}={(1+{\gamma }_{\text{cjs}}\sqrt{54}\frac{\mathrm{det}(s)}{{s}_{\mathrm{II}}^{3}})}^{1/6}\) eq 3.2.1.2-2
\({h}_{c}^{0}=h(\theta =\frac{\pi }{3})={(1-{\gamma }_{\text{cjs}})}^{1/6}\)
\({h}_{t}^{0}={(1+{\gamma }_{\text{cjs}})}^{1/6}\)
\(g(s)={s}_{\mathrm{II}}h(\theta )\) eq 3.2.1.2-3
\(u(\sigma ,{\gamma }^{p})=-\frac{m({\gamma }^{p})k({\gamma }^{p})}{\sqrt{6}{\sigma }_{c}}\frac{g(s)}{{h}_{c}^{0}}-\frac{m({\gamma }^{p})k({\gamma }^{p})}{3{\sigma }_{c}}{I}_{1}+s({\gamma }^{p})\mathrm{.}k({\gamma }^{p})\) eq 3.2.1.2-4
Note:
We demonstrate [Annexe 1] the equivalence of the two expressions
We show that a second formulation of the criterion with a realignment to a triaxial in compression and in extension is possible but we do not choose it. However, it is presented in chapter [§9].
3.2.1.3. Allure of the thresholds#
The shape of the thresholds is traced to the peak criterion and to the ultimate criterion.
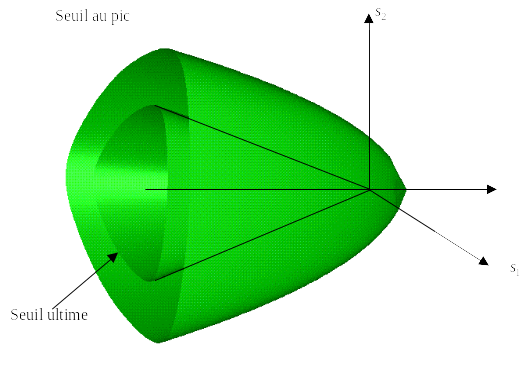
3.2.2. Work hardening#
To translate the post-peak softening of the rock, laws of variation of the parameters m, s and a of the criterion are defined as a function of the internal work-hardening variable \({\gamma }^{p}\) (this is the cumulative plastic deviatory deformation, proportional to the second invariant of the deviatory deformation tensor, corresponding to the plastic distortion).
\(\begin{array}{cc}s({\gamma }^{p})=(1-\frac{{\gamma }^{p}}{{\gamma }^{e}})& \text{si}{\gamma }^{p}<{\gamma }_{e}\\ s({\gamma }^{p})=0& \text{si}{\gamma }^{p}\ge {\gamma }_{e}\end{array}\) eq 3.2.2-1
: label: EQ-None
text {if}underline {{gamma}} ^ {p} > {gamma} _ {text {ult}}}}
Sinon
\(\Omega ({\gamma }^{p})={(\frac{{\gamma }^{p}}{{\gamma }^{e}})}^{\eta }\frac{{a}_{e}-{a}_{\text{pic}}}{1-{a}_{e}}\frac{{\gamma }_{\text{ult}}-{\gamma }_{e}}{{\gamma }_{\text{ult}}-{\gamma }^{p}}\) eq 3.2.2-2
\(a({\gamma }^{p})=\frac{{a}_{\text{pic}}+\Omega ({\gamma }^{p})}{1+\Omega ({\gamma }^{p})}\) eq 3.2.2-3
\(\begin{array}{cc}m({\gamma }^{p})=\frac{{\sigma }_{c}}{{\sigma }_{\text{p1}}}\left[{({m}^{\text{pic}}\frac{{\sigma }_{\text{p1}}}{{\sigma }_{c}}+1)}^{\frac{{a}_{\text{pic}}}{a({\gamma }^{p})}}-s({\gamma }^{p})\right]& \text{si}{\gamma }^{p}<{\gamma }_{e}\\ m({\gamma }^{p})=\frac{{\sigma }_{c}}{{\sigma }_{\text{p2}}}\left[{({m}_{e}\frac{{\sigma }_{\text{p2}}}{{\sigma }_{c}})}^{\frac{{a}_{\text{pic}}}{a({\gamma }^{p})}}\right]& \text{si}{\gamma }^{p}\ge {\gamma }_{e}\end{array}\) eq 3.2.2-4
\(k({\gamma }^{p})={(\frac{2}{3})}^{\frac{1}{\mathrm{2a}({\gamma }^{p})}}\). eq 3.2.2-5
These laws of evolution for each of the 3 parameters are dependent on each other and respect the conditions of intersection of the criteria during the work hardening phase [bib1].
Note:
3.2.3. Law of dilatance#
3.2.3.1. Generalized writing#
The law of dilatance (it is accepted that the value of dilatance is inversely proportional to that of cohesion) can be generalized by writing:
\(\mathrm{sin}\psi =\mathrm{sin}(\psi ({\alpha }^{\text{'}}))=\gamma \frac{{\alpha }^{\text{'}}-{m}_{\text{ult}}-1}{\zeta {\alpha }^{\text{'}}+{m}_{\text{ult}}+1}\) eq 3.2.3.1-1
with:
\({\alpha }^{\text{'}}={\alpha }^{\text{'}}({I}_{\mathrm{1,}}g(s),{\sigma }_{\text{t0}})=\frac{\tilde{{\sigma }_{1}}-{\sigma }_{\text{t0}}}{\tilde{{\sigma }_{3}}-{\sigma }_{\text{t0}}}\) eq 3.2.3.1-2
\({s}_{3}=\sqrt{\frac{2}{3}}{s}_{\text{II}}\mathrm{cos}(\theta );\text{}{s}_{1}=\sqrt{\frac{2}{3}}{s}_{\text{II}}\mathrm{cos}(\theta +\frac{2\pi }{3});\text{}{s}_{2}=\sqrt{\frac{2}{3}}{s}_{\text{II}}\mathrm{cos}(\theta -\frac{2\pi }{3});\) where \(\theta\) is the Lode angle
\({\sigma }_{1}=\frac{{I}_{1}}{3}+{s}_{1};\text{}{\sigma }_{2}=\frac{{I}_{1}}{3}+{s}_{2};\text{}{\sigma }_{3}=\frac{{I}_{1}}{3}+{s}_{3};\text{}\)
\(\{\begin{array}{}\tilde{{\sigma }_{1}}={\sigma }_{i}\text{avec}i\text{tel que}\mid {\sigma }_{i}\mid =\text{max}(\mid {\sigma }_{j}\mid ,j=\mathrm{1,2}\mathrm{,3})\\ \tilde{{\sigma }_{3}}={\sigma }_{i}\text{avec}i\text{tel que}\mid {\sigma }_{i}\mid =\text{max}(\mid {\sigma }_{j}\mid ,j=\mathrm{1,2}\mathrm{,3})\end{array}\)
Note:
A condition to be met is that the ratio \(\frac{\gamma }{\zeta }\) remains less than 1. In the case of very resistant hard rocks, subject to relatively low confinement stresses, the law of dilatance can thus tend towards this ratio. If the two parameters are unitary, we find the expression of Rowe’s law describing the law of dilatance for powdery soils. This approach amounts to maintaining the same expression as for a heavily damaged rock, by assimilating the effect of cohesion to that of an additional containment of value \({\sigma }_{\mathrm{t0}}\).
Characterization \({\sigma }_{\mathrm{t0}}\) according to the parameters (a, m, s) characterizing the rock
Case where \(s({\gamma }^{p})=0\)
Disappearance of cohesion, we ask \({\sigma }_{\mathrm{t0}}=0\)
Case where \(s({\gamma }^{p})\ne 0\)
\({\sigma }_{\mathrm{t0}}={\sigma }_{\mathrm{t0}}({\varphi }_{\mathrm{0,}}{C}_{0})={\mathrm{2C}}_{0}\sqrt{\frac{1-\mathrm{sin}{\varphi }_{0}}{1+\mathrm{sin}{\varphi }_{0}}}\) eq 3.2.3.1-3
with:
\(\{\begin{array}{}{\varphi }_{0}={\varphi }_{0}(m,s,a)=2\cdot \mathrm{arctan}(\sqrt{1+{\text{ams}}^{a-1}})-\frac{\pi }{2}\\ {C}_{0}={C}_{0}(m,s,a)=\frac{{\sigma }_{c}{s}^{a}}{\sqrt{1+{\text{ams}}^{a-1}}}\end{array}\)
3.2.3.2. Determining the intersection of the intermediate criterion and the ultimate criterion#
By writing the continuity of \(m\) in \({\gamma }_{\text{ult}}\) we get the following relationship:
\(m({\gamma }_{\text{ult}})=\frac{{\sigma }_{c}}{{\sigma }_{\text{p2}}}\left[{({m}_{e}\frac{{\sigma }_{\text{p2}}}{{\sigma }_{c}})}^{\frac{{a}_{e}}{a({\gamma }_{\text{ult}})}}\right]\)
\({m}_{\text{ult}}=\frac{{\sigma }_{c}}{{\sigma }_{\text{p2}}}{({m}_{e}\frac{{\sigma }_{\text{p2}}}{{\sigma }_{c}})}^{\frac{{a}_{e}}{{a}_{\text{ult}}}}\)
\({m}_{\text{ult}}={m}_{e}^{{a}_{e}}{(\frac{{\sigma }_{\text{p2}}}{{\sigma }_{c}})}^{{a}_{e}-1}\)
\({\sigma }_{\text{p2}}={\sigma }_{c}{(\frac{{m}_{\text{ult}}}{{m}_{e}^{{a}_{e}}})}^{\frac{1}{{a}_{e}-1}}\) eq 3.2.3.2-1
3.2.4. Plastic flow#
The formalism adopted is rewritten based on the CJS model [R7.01.13]. When the stresses reach the edge of the reversibility domain, plastic deformations develop. To calculate them, there is a potential function controlling the evolution of deformations and defined by the relationship \(\dot{{\varepsilon }^{p}}=\dot{\lambda }G\) where \(\dot{\lambda }\) is the plastic multiplier and
\(G=\frac{\partial f}{\partial \sigma }-(\frac{\partial f}{\partial \sigma }n)n\). eq 3.2.4-1
The potential function is obtained from the following kinematic condition:
\(\dot{{\varepsilon }_{\nu }^{p}}=-{\beta }^{\text{'}}\frac{{\mathrm{s.}\dot{\varepsilon }}^{p}}{{s}_{\mathrm{II}}}\) eq 3.2.4-2
The dilatance parameter \({\beta }^{\text{'}}\) is calculated from the dilatance angle \(\psi\) (defined by [éq 3.2.3.1-1]) by the formula:
\(\begin{array}{}{\beta }^{\text{'}}={\beta }^{\text{'}}(\psi )=-\frac{2\sqrt{6}\mathrm{sin}(\psi )}{3-\mathrm{sin}(\psi )}\\ {\beta }^{\text{'}}=0\text{si}{\gamma }^{p}>{\gamma }_{\text{ult}}(1-{10}^{\text{-3}})\end{array}\) eq 3.2.4-3
Note:
\({\beta }^{\text{'}}\) is positive when \({\gamma }^{p}=0\) and in compression, then it becomes negative when plasticity develops. It is always negative under traction
It is then possible to try to express the kinematic condition [éq 3.2.4-2] using a tensor
in the form:
\({\mathrm{n.}\dot{\varepsilon }}^{p}=0\) eq 3.2.4-4
After decomposing each term into deviatory and hydrostatic parts, we find the expression:
\(({n}_{I}{s}_{\text{ij}}+{n}_{2}{\delta }_{\text{ij}})\text{.}(\dot{{e}_{\text{ij}}^{p}}+\frac{1}{3}\dot{{\varepsilon }_{\nu }^{p}}{\delta }_{\text{ij}})={n}_{1}{s}_{\text{ij}}\dot{{e}_{\text{ij}}^{p}}+{n}_{2}\dot{{\varepsilon }_{\nu }^{p}}=0\)
We deduce the relationship \(\frac{{n}_{1}}{{n}_{2}}=\frac{{\beta }^{\text{'}}}{{s}_{\text{II}}}\) which, added to the condition for normalizing the tensor
, leads to the expression:
\(n=\frac{{\beta }_{\text{'}}\frac{s}{{s}_{\text{II}}}+I}{\sqrt{{\beta }^{\text{'2}}+3}}\) eq 3.2.4-5
The law of evolution of
must be such that the kinematic condition is satisfied. It is therefore proposed to take the screening of
upon
(normal hypersurface deformation), i.e.:
\(\dot{{\varepsilon }^{p}}=\dot{\lambda }G=\dot{\lambda }(\frac{\partial f}{\partial \sigma }-(\frac{\partial f}{\partial \sigma }n)n)\)
The condition relating to plastic volume deformation is also deduced from this:
\(\dot{{\varepsilon }_{\nu }^{p}}=\dot{\lambda }G\) eq 3.2.4-6