6. Aster Springs#
6.1. List of routines changed and added#
Only the nmcomp.f routine has been modified. When behavior CJS is chosen, it allows you to call the nmcjs.f routine, the starting point for integrating the law.
The set of Fortran routines developed as part of the integration of the CJS law into the Code_Aster is as follows:
cjsc3q.f, cjsci1.f, cjsdtd.f, cjsela.f, cjside.f, cjsiid.f, cjsiid.f,
cjsjde.f, cjsjid.f, cjsjis.f, cjsmat.f, cjsmde.f, cjsmid.f,
cjsmis.f, cjsnor.f, cjspla.f, cjsqco.f, cjsqij.f, cjssmd.f, cjssmd.f,
cjssmi.f, cjst.f, cjstde.f, cjstel.f, cjstid.f, cjstis.f, cjstis.f,
lcdete.f, nmcjs.f, cjsinp.f, cjsncn.f, cjsncv.f, cjsnvi.f, cjsnvi.f,
cjsqq.f.
6.2. General flow chart of the main routines#
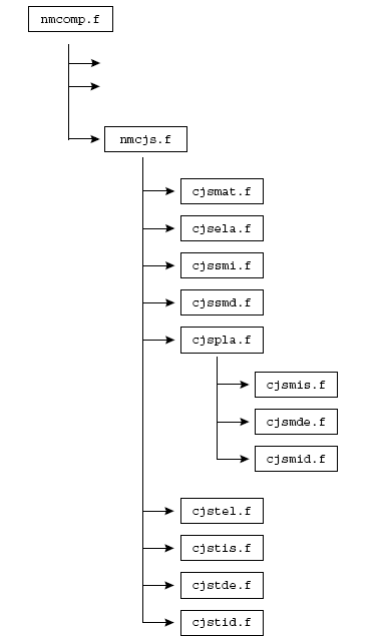
The main FORTRAN routines for integrating the CJS law are linked as follows:
6.3. Details of the functionalities of the FORTRAN routines developed#
6.3.1. Routine: CJSC3Q#
Objective: calculating \(\text{cos}(3{\mathrm{\theta }}_{q})\)
Input and output variables:
IN SIG: CONTRAINTES
X: VARIABLES ECROUI CINE BY: PRESS ATMOSPHERIQUE (DONNEE MATERIAU)
OUT Q: DEV (SIG) - TRACE (SIG) *X
QII: SQRT (QIJ * QIJ) COS3TQ: SQRT (54) *DET (Q)/(QII**3)
6.3.2. Routine: CJSCI1#
Objective:
solving equation \({I}_{1}^{+}-{I}_{1}^{-}-3{K}_{o}^{e}{(\frac{{I}_{1}^{+}}{3{P}_{a}})}^{n}\text{tr}(\Delta \varepsilon )=0\) by the secant method, for nonlinear elastic behavior
Input and output variables:
IN CRIT: CRITERES OF CONVERGENCE
MATER: COEFFICIENTS MATERIAU A T+DT DEPS: INCREMENT FROM DEFORMATION SIGD: CONTRAINTE A T
OUT I1: TRACE FROM SIG TO T+DT
TRACT: VARIABLE LOGIQUE INDIQUANT THE TRACTION
6.3.3. Routine: CJSDTD#
Objective:
Calculation of the derivative of the tensor \({t}^{d}\) with respect to \(q\)
Input and output variables:
IN MOD: MODELISATION
Q: TENSEUR (6 COMPOSANTES)
OUT DTDDQ: TENSEUR RESULTAT (6 COMPOSANTES)
6.3.4. Routine: CJSELA#
Objective:
nonlinear elastic calculation of stresses
Input and output variables:
IN MOD: MODELISATION
CRIT: CRITERES FROM CONVERGENCE MATERF: COEFFICIENTS MATERIAU A T+DT SIGD: CONTRAINTE A T DEPS: INCREMENT FROM DEFORMATION
OUT SIGF: CONTRAINTE A T+DT
Organization of CJSELA
calculation of the first invariant of the constraints I1 at t+dt:
call from CJSCI1
calculation of the elastic matrix coefficients and assembly of the matrix
calculation of the increment of stresses and stresses at t+dt:
call from LCPRMV and LCSOVE
6.3.5. Routine: CJSIDE#
Objective:
for the integration of the deviatory plastic mechanism, calculation of a test solution in order to then start the local Newton iterations.
Input and output variables:
IN MOD: MODELISATION
MATER: COEFFICIENTS MATERIAU A T+DT EPSD: DEFORMATION AT T+DT DEPS: INCREMENT FROM DEFORMATION YD: VARIABLES A T = (SIGD, VIND, LAMB)
VAR GD: TENSEUR FROM THE LOI D ECOULEMENT PLASTIQUE DEV.
OUT DY: SOLUTION D ESSAI
Organization of CJSIDE
calculation of the elastic operator,
calculation of work hardening laws \({G}^{R}\) and \({G}^{X}\),
calculation of the flow law of the plastic deviatory mechanism \({G}^{d}\),
calculation of the threshold \({f}^{d}\), its derivative \(\frac{\partial {f}^{d}}{\partial {\mathrm{\Delta \lambda }}^{d}}\) and the plastic multiplier \({\mathrm{\Delta \lambda }}^{d}\),
calculation of the test solution
6.3.6. Routine: CJSIID#
Objective:
for the simultaneous integration of isotropic and deviatory plastic mechanisms, calculation of a test solution in order to then start local Newton iterations.
Input and output variables:
IN MOD: MODELISATION
MATER: COEFFICIENTS MATERIAU A T+DT EPSD: DEFORMATION AT T+DT DEPS: INCREMENT FROM DEFORMATION YD: VARIABLES A T = (SIGD, VIND, LAMB)
VAR GD: TENSEUR FROM THE LOI D ECOULEMENT PLASTIQUE DEV.
OUT DY: SOLUTION D ESSAI
Organization of CJSIID
calculation of the elastic operator,
calculation of work hardening laws \({G}^{R}\) and \({G}^{X}\),
calculation of the flow law of the plastic deviatory mechanism \({G}^{d}\),
calculation of the thresholds \({f}^{i}\) and \({f}^{d}\), of their derivatives \(\frac{\partial {f}^{i}}{\partial {\mathrm{\Delta \lambda }}^{i}}\), \(\frac{\partial {f}^{i}}{\partial {\mathrm{\Delta \lambda }}^{d}}\), \(\frac{\partial {f}^{d}}{\partial {\mathrm{\Delta \lambda }}^{i}}\) and \(\frac{\partial {f}^{d}}{\partial {\mathrm{\Delta \lambda }}^{d}}\), and of the plastic multipliers \({\mathrm{\Delta \lambda }}^{i}\) and \({\mathrm{\Delta \lambda }}^{d}\),
calculation of the test solution
6.3.7. Routine: CJSJDE#
Objective:
calculation of \(\text{DRDY}\) and \(R\) for the resolution of \(\frac{\text{DR}}{\text{DY}}({Y}^{p}){\text{DY}}^{\text{p+1}}=-R({Y}^{p})\) (plastic deviatory mechanism)
Input and output variables:
IN MOD: MODELISATION
MATER: COEFFICIENTS MATERIAU A T+DT EPSD: DEFORMATION A T DEPS: INCREMENT FROM DEFORMATION YD: VARIABLES A T = (SIGD, VIND, LAMBDD) YF: VARIABLES A T+DT = (SIGF, VINF, LAMBDF)
VAR GD: TENSEUR FROM THE LOI D ECOULEMENT PLASTIQUE DEV.
OUT R: SECOND MEMBRE
SIGNE: SIGNE FROM S: DEPSDP DRDY: JACOBIEN
Organization of CJSJDE
calculation of the elastic operator,
calculation of work hardening laws \({G}^{R}\) and \({G}^{X}\),
calculation of the flow law of the plastic deviatory mechanism \({G}^{d}\),
calculation of multiple intermediate derivatives
calculation of terms \(\frac{\partial {G}^{R}}{\partial {\mathrm{\sigma }}_{\text{ij}}}\), \(\frac{\partial {G}^{R}}{\partial R}\), \(\frac{\partial {G}_{\text{mn}}^{X}}{\partial {\mathrm{\sigma }}_{\text{ij}}}\), \(\frac{\partial {G}_{\text{mn}}^{X}}{\partial {X}_{\text{ij}}}\),,, \(\frac{\partial {G}_{\text{mn}}^{d}}{\partial {\mathrm{\sigma }}_{\text{ij}}}\), \(\frac{\partial {G}_{\text{mn}}^{d}}{\partial R}\), \(\frac{\partial {G}_{\text{mn}}^{d}}{\partial {X}_{\text{ij}}}\)
calculation of the components of \(\text{DRDY}\) and \(R\)
assembly of \(\text{DRDY}\) and \(R\)
6.3.8. Routine: CJSJID#
Objective:
calculation of \(\text{DRDY}\) and \(R\) for the resolution of \(\frac{\text{DR}}{\text{DY}}({Y}^{p}){\text{DY}}^{\text{p+1}}=-R({Y}^{p})\) (isotropic and deviatory plastic mechanisms)
Input and output variables:
IN MOD: MODELISATION
MATER: COEFFICIENTS MATERIAU A T+DT EPSD: DEFORMATION A T DEPS: INCREMENT FROM DEFORMATION YD: VARIABLES A T = (SIGD, VIND, LAMBDD) YF: VARIABLES A T+DT = (SIGF, VINF, LAMBDF)
VAR GD: TENSEUR FROM THE LOI D ECOULEMENT PLASTIQUE DEV.
OUT R: SECOND MEMBRE
SIGNE: SIGNE FROM S: DEPSDP DRDY: JACOBIEN
Organization of CJSJID
calculation of the elastic operator,
calculation of work hardening laws \({G}^{{Q}_{\text{iso}}}\), \({G}^{R}\) and \({G}^{X}\),
calculation of the flow law of the plastic deviatory mechanism \({G}^{d}\),
calculation of multiple intermediate derivatives
calculation of the terms \(\frac{\partial {G}^{{Q}_{\text{iso}}}}{\partial {Q}_{\text{iso}}}\), \(\frac{\partial {G}^{R}}{\partial {\mathrm{\sigma }}_{\text{ij}}}\), \(\frac{\partial {G}^{R}}{\partial R}\), \(\frac{\partial {G}_{\text{mn}}^{X}}{\partial {\mathrm{\sigma }}_{\text{ij}}}\),, \(\frac{\partial {G}_{\text{mn}}^{X}}{\partial {X}_{\text{ij}}}\),, \(\frac{\partial {G}_{\text{mn}}^{d}}{\partial {\mathrm{\sigma }}_{\text{ij}}}\), \(\frac{\partial {G}_{\text{mn}}^{d}}{\partial R}\), \(\frac{\partial {G}_{\text{mn}}^{d}}{\partial {X}_{\text{ij}}}\)
calculation of the components of \(\text{DRDY}\) and \(R\)
assembly of \(\text{DRDY}\) and \(R\)
6.3.9. Routine: CJSJIS#
Objective:
calculation of \(\text{DRDY}\) and \(R\) for the resolution of \(\frac{\text{DR}}{\text{DY}}({Y}^{p}){\text{DY}}^{\text{p+1}}=-R({Y}^{p})\) (isotropic plastic mechanism)
Input and output variables:
IN MOD: MODELISATION
MATER: COEFFICIENTS MATERIAU A T+DT DEPS: INCREMENT FROM DEFORMATION YD: VARIABLES A T = (SIGD, VIND, LAMBDD) YF: VARIABLES A T+DT = (SIGF, VINF, LAMBDF)
OUT R: SECOND MEMBRE
DRDY: JACOBIEN
Organization of CJSJIS
calculation of the elastic operator,
calculation of the components of \(\text{DRDY}\) and \(R\)
assembly of \(\text{DRDY}\) and \(R\)
6.3.10. Routine: CJSMAT#
Objective:
retrieving material data, the number of field components, the number of internal variables and the CJS level chosen.
Input and output variables:
IN IMAT: ADRESSE FROM MATERIAU CODE
MOD: TYPE FROM MODELISATION TEMPF: TEMPERATURE AT T+DT
OUT MATERF: COEFFICIENTS MATERIAU A T+DT
NDT: NB TOTAL OF COMPOSANTES TENSEURS NDI: NUMBER OF COMPOSANTES DIRECTES TENSEURS NVI: NUMBER OF VARIABLES INTERNES NIVCJS: NIVEAU 1, 2, OR 3 OF THE LOI CJS
Organization of CJSMAT
retrieving the number of field components and the number of internal variables according to the modeling chosen,
material data recovery,
recognition of the CJS level chosen according to the parameters given.
6.3.11. Routine: CJSMDE#
Objective:
elasto-plastic calculation of stresses with the plastic deviatory mechanism activated: resolution by Newton’s method of \(R(Y)=0\)
Input and output variables:
IN MOD: MODELISATION
CRIT: CRITERES FROM CONVERGENCE MATER: COEFFICIENTS MATERIAU A T+DT NVI: NUMBER OF VARIABLES INTERNES EPSD: DEFORMATIONS A T DEPS: INCREMENT FROM DEFORMATION SIGD: CONTRAINTE A T VIND: VARIABLES INTERNES A T STOPNC: ARRET IN CAS OF NON CONVERGENCE
VAR SIGF: CONTRAINTE A T+DT
VINF: VARIABLES INTERNES A T+DT NOCONV: PAS FROM CONVERGENCE
Organization of CJSMDE
initialization of \(\text{YD}\) by the state at t
calculation of a test solution with CJSIDE
loop over Newton iterations
increment \(\text{YF}=\text{YD}+\text{DY}\)
calculation of \(\text{DRDY}\) and \(R\): CJSJDE
system resolution using the Gauss method: MTGAUS
update of the \(\text{DY}\) solution
convergence test
update of constraints and internal variables
6.3.12. Routine: CJSMID#
Objective:
elasto-plastic calculation of stresses with activated isotropic and deviatory plastic mechanisms: resolution by Newton’s method of \(R(Y)=0\)
Input and output variables:
IN MOD: MODELISATION
CRIT: CRITERES FROM CONVERGENCE MATER: COEFFICIENTS MATERIAU A T+DT NVI: NUMBER OF VARIABLES INTERNES EPSD: DEFORMATIONS A T DEPS: INCREMENT FROM DEFORMATION SIGD: CONTRAINTE A T VIND: VARIABLES INTERNES A T STOPNC: ARRET IN CAS OF NON CONVERGENCE
VAR SIGF: CONTRAINTE A T+DT
VINF: VARIABLES INTERNES A T+DT NOCONV: PAS FROM CONVERGENCE
Organization of CJSMID
initialization of \(\text{YD}\) by the state at t
calculation of a test solution with CJSIID
loop over Newton iterations
increment \(\text{YF}=\text{YD}+\text{DY}\)
calculation of \(\text{DRDY}\) and \(R\): CJSJID
system resolution using the Gauss method: MTGAUS
update of the \(\text{DY}\) solution
convergence test
update of constraints and internal variables
6.3.13. Routine: CJSMIS#
Objective:
elasto-plastic stress calculation with the activated isotropic plastic mechanism: Newton’s method resolution of \(R(Y)=0\)
Input and output variables:
IN MOD: MODELISATION
CRIT: CRITERES FROM CONVERGENCE MATER: COEFFICIENTS MATERIAU A T+DT DEPS: INCREMENT FROM DEFORMATION SIGD: CONTRAINTE A T VIND: VARIABLES INTERNES A T STOPNC: ARRET IN CAS OF NON CONVERGENCE
VAR SIGF: CONTRAINTE A T+DT
VINF: VARIABLES INTERNES A T+DT NOCONV: PAS FROM CONVERGENCE
Organization of CJSMIS
initialization of \(\text{YD}\) by elastic prediction
loop over Newton iterations
increment \(\text{YF}=\text{YD}+\text{DY}\)
calculation of \(\text{DRDY}\) and \(R\): CJSJIS
resolution of the system by the Gauss method: MTGAUS
update of solution \(\text{DY}\)
convergence test
update of constraints and internal variables
6.3.14. Routine: CJSNOR#
Objective:
Calculating a vector parallel to \(\frac{\partial {f}^{d}}{\partial {q}_{\text{ij}}}\)
Input and output variables:
IN MATER: MATERIAU
SIG: CONTRAINTES X: VARIABLES INTERNES CINEMATIQUES
OUT NOR: ESTIMATION OF THE DITRECTION OF THE NORMALE
TO THE SURFACE DEVIATOIRE DANS THE PLAN DEVIATOIRE PERPENDICULAIRE AT TRISECTRICE THE VECTEUR NOR (1: NDT) N EST PAS NORME SA NORME EST NOR (NDT +1)
6.3.15. Routine: CJSPLA#
Objective:
elasto-plastic calculation of stresses.
Input and output variables:
IN MOD: MODELISATION
CRIT: CRITERES FROM CONVERGENCE MATER: COEFFICIENTS MATERIAU A T+DT SEUILI: FONCTION FROM CHARGE ISO. CALCULEE AVEC PREDICT ELAS SEUILD: FONCTION FROM CHARGE DEV. CALCULEE AVEC PREDICT ELAS NVI: NOMBRE FROM VARIABLES INTERNES EPSD: DEFORMATIONS A T DEPS: INCREMENT FROM DEFORMATION SIGD: CONTRAINTE A T VIND: VARIABLES INTERNES A T
VAR SIGF: CONTRAINTE A T+DT (IN -> ELAS, OUT -> PLASTI)
OUT VINF: VARIABLES INTERNES A T+DT
MECANI: MECANISME (S) ACTIVE (S)
Organization of CJSPLA
hypothesis on the plastic mechanism (s) activated as a function of the values of the thresholds \({f}^{i}\) and \({f}^{d}\) calculated from elastic prediction,
processing the possible redistribution of the time step
saving the elastic prediction,
elasto-plastic calculation,
isotropic plastic mechanism: CJSMIS
diverting plastic mechanism: CJSMDE
isotropic and deviatory plastic mechanisms simultaneously: CJSMID
calculation of thresholds from the constraints at t+dt
call of CJSSMI and CJSSMD
if (hypothesis of an isotropic mechanism and \({f}^{d}\) positive) or (hypothesis of a deviatory mechanism and \({f}^{i}\) positive): return to elasto-plastic calculation with isotropic and deviatory plastic mechanisms simultaneously,
otherwise end of routine
6.3.16. Routine: CJSQCO#
Objective:
CJS utility routine allowing the calculation of standard quantities listed below
Input and output variables:
IN GAMMA: PARAMETRE MATERIAU
SIG: CONTRAINTES X: VARIABLES ECROUI CINE PREF: PRESS REF POUR NORMALISATION EPSSIG: EPSILON POUR NULLITE DEVIATEUR I1: TRACE FROM TENSEUR DES CONTRAINTES
OUT S: DEV (SIG)
SII: SQRT (S:S) SIIREL: SII/PREF COS3TS: LODE (SIG) HTS: FONCTION H (TETHA_S) DETS: DETERMINANT OF S Q: Q (SIG -X) QII: SQRT (Q:Q) QIIREL: QII/PREF COS3TQ HTQ: FONCTION H (TETHA_Q) DETQ: DETERMINANT FROM Q
6.3.17. Routine: CJSQIJ#
Objective:
Calculating tensor \({q}_{\text{ij}}\)
Input and output variables:
IN N: DIMENSION OF S, X, Q
S: DEVIATEUR I1: PREMIER INV. X: CENTRE OF THE SURFACE OF CHARGE DEVIATOIRE
OUT Q: TENSEUR RESULTAT
6.3.18. Routine: CJSSMD#
Objective:
calculation of the threshold of the deviatory plastic mechanism.
Input and output variables:
IN SIG: CONTRAINTE
VIN: VARIABLES INTERNES
OUT SEUILD: SEUIL ELASTICITE FROM MECANISME DEVIATOIRE
6.3.19. Routine: CJSSMI#
Objective:
calculation of the threshold of the isotropic plastic mechanism.
Input and output variables:
IN SIG: CONTRAINTE
VIN: VARIABLES INTERNES
OUT SEUILI: SEUIL ELASTICITE FROM MECANISME ISOTROPE
6.3.20. Routine: CJST#
Objective:
Calculation of \(t\) = \(\frac{\partial \text{det}s}{\partial s}\).
Input and output variables:
IN S: MATRICE
OUT T: T (SOUS FORME VECTORIELLE AVEC RAC2)
6.3.21. Routine: CJSTDE#
Objective:
Calculation of the tangent matrix for the deviatory plastic mechanism
Input and output variables:
IN MOD: MODELISATION
MATER: COEFFICIENTS MATERIAU NVI: NUMBER OF VARIABLES INTERNES EPS: DEFORMATIONS SIG: CONTRAINTES VIN: VARIABLES INTERNES
OUT DSDESY: MATRICE TANGENTE SYMETRISEE
Organization of CJSTDE
calculation of the elastic operator,
calculation of work hardening laws \({G}^{R}\) and \({G}^{X}\),
calculation of the flow law of the plastic deviatory mechanism \({G}^{d}\),
calculation of intermediate terms
calculation of the tangent matrix
symmetrization of the tangent matrix
6.3.22. Routine: CJSTEL#
Objective:
Calculation of the tangent matrix for the elastic mechanism
Input and output variables:
IN MOD: MODELISATION
MATER: COEFFICIENTS MATERIAU SIG: CONTRAINTES
OUT HOOK: OPERATEUR RIGIDITE ELASTIQUE
Organization of CJSTEL
elastic operator calculation
6.3.23. Routine: CJSTID#
Objective:
Calculation of the tangent matrix for isotropic and deviatory plastic mechanisms
Input and output variables:
IN MOD: MODELISATION
MATER: COEFFICIENTS MATERIAU NVI: NUMBER OF VARIABLES INTERNES EPS: DEFORMATIONS SIG: CONTRAINTES VIN: VARIABLES INTERNES
OUT DSDESY: MATRICE TANGENTE SYMETRISEE
Organization of CJSTEL
calculation of the elastic operator,
calculation of work hardening laws \({G}^{R}\) and \({G}^{X}\),
calculation of the flow law of the plastic deviatory mechanism \({G}^{d}\),
calculation of intermediate terms
calculation of the tangent matrix
symmetrization of the tangent matrix
6.3.24. Routine: CJSTIS#
Objective:
Calculation of the tangent matrix for the isotropic plastic mechanism
Input and output variables:
IN MOD: MODELISATION
MATER: COEFFICIENTS MATERIAU SIG: CONTRAINTES VIN: VARIABLES INTERNES
OUT DSDE: MATRICE TANGENTE
Organization of CJSTEL
calculation of the tangent matrix
6.3.25. Routine: LCDETE#
Objective:
Calculation of a determinant matrix 33
Input and output variables:
IN A: MATRICE
OUT LCDETE: DETERMINANT
6.3.26. Routine: NMCJS#
Objective:
realization of the integration of law CJS: calculation of the stresses at t+dt and/or of the tangent matrix, depending on the calculation option chosen.
Input and output variables:
IN TYPMOD TYPE FROM MODELISATION
IMAT ADRESSE FROM MATERIAU CODE COMP COMPORTEMENT BY L ELEMENT CRIT CRITERES LOCAUX INSTAM INSTANT T INSTAP INSTANT T+DT TEMPM TEMPERATURE A T TEMPF TEMPERATURE A T+DT TREF TEMPERATURE FROM REFERENCE EPSD DEFORMATION TOTALE A T DEPS INCREMENT FROM DEFORMATION TOTALE SIGD CONTRAINTE A T VIND VARIABLES INTERNES A T + INDICATEUR ETAT T OPT OPTION FROM CALCUL TO FAIRE
OUT SIGF CONTRAINTE A T+DT
VINF VARIABLES INTERNES A T+DT + INDICATEUR ETAT T+DT DSDE MATRICE FROM COMPORTEMENT TANGENT TO T+DT OR T
Organization of NMCJS
retrieving material data, the number of field components, the number of internal variables and the chosen CJS level:
call from CJSMAT
blocking of internal variables according to the level CJS chosen
calculation of the stresses at t+dt
elastic prediction: CJSELA
calculation of the thresholds of isotropic and deviatory mechanisms: CJSSMI and CJSSMD
if one of the thresholds is exceeded, elasto-plastic calculation: CJSPLA
calculation of the tangent matrix according to the mechanism involved
elastic: CJSTEL
isotropic plastic: CJSTIS
Deviatory plastic: CJSTDE
isotropic and deviatory plastic: CJSTID