1. Introduction

1.1. Nonlinearity and Newton’s failure

The Newton method presented in [R5.03.01] fails on some problems that show a structure response that is not strictly monotonic depending on the movements or loads imposed. In the figure, the case is shown where, for a given load level, there are several alternative displacements. This problem is therefore not solvable with Newton if we manage the loading problem.

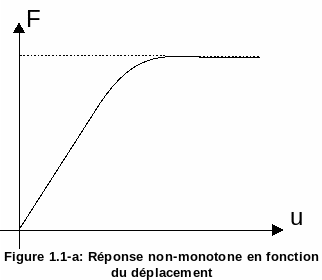
Figure 1.1-a : Non-monotonic response as a function of displacement

A second case (figure) concerns non-linear geometric problems (typically the buckling of thin shells and « soft » snap-back problems). In this case, for a level of loading, we have several solutions while moving and for a level of movement we have several possible loads. This problem cannot be solved directly by Newton’s method, whether by driving while loading or when moving.

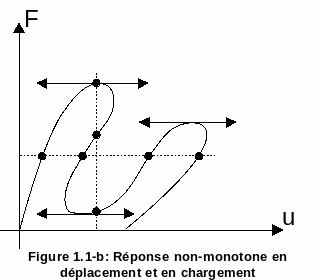
Figure 1.1-b : Non-monotonic response when moving and loading

The third case (figure) describes damage problems in which sudden elastic returns (corresponding to the progressive damage of the material) make the curve very irregular (« sudden » snap-backs)

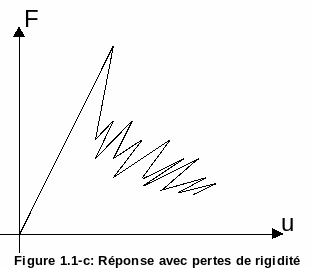
Figure 1.1-c : Response with stiffness loss

Finally, there is finally a whole category of problems in which the loss of ellipticity of the problem creates bifurcations and therefore branches of different solutions (see figure). In this case, what interests the engineer the most is generally the dissipative branch and not the elastic branch. We will see that there are techniques for selecting the « right » branches.

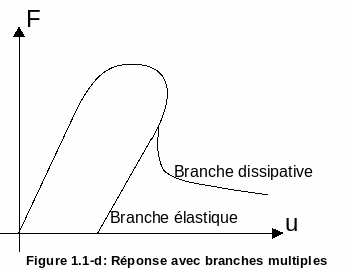
Figure 1.1-d : Answer with multiple branches

1.2. Problems with unknown load intensity

Control can also be used in the case where the problem shows, through its natural data, an additional unknown, which is the intensity of the load applied. Control makes it possible to deal with the case where only the direction and the point of application of the load are known, the intensity remaining an unknown of the problem. For example, in the figure, we see the case of a cable stretched between two pylons. We know that it is necessary to apply a loading that pulls the cable (we therefore know the point of application and the direction of the loading) but we do not know the intensity \(\eta\) to be applied to obtain a given \(f\) arrow.

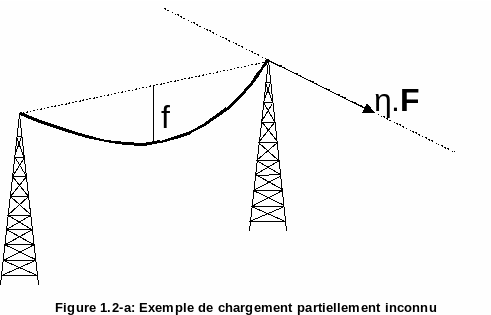
Figure 1.2-a : Partially unknown loading example