1. Field of application#

1.1. Purpose#

In parallel, the law of behavior KICHENIN_NL combines an elastoplastic model with linear kinematic work hardening with a Maxwell viscoelastic model whose shock absorber is non-linear, such as the Norton type. A rheological illustration is given below. It was originally dedicated to the description of polyethylene but can undoubtedly be applied to other materials.

This behavior model is compatible with a kinematics of small disturbances (PETIT) or large deformations (GDEF_LOG).

Finally, this model describes the stress response as an explicit function of deformation and internal variables and not as a law of evolution under incremental stress. The constraint does not contribute to defining the mechanical state of the system, it is a consequence of this (in particular, the constraint does not contribute to the definition of an initial state of the system).

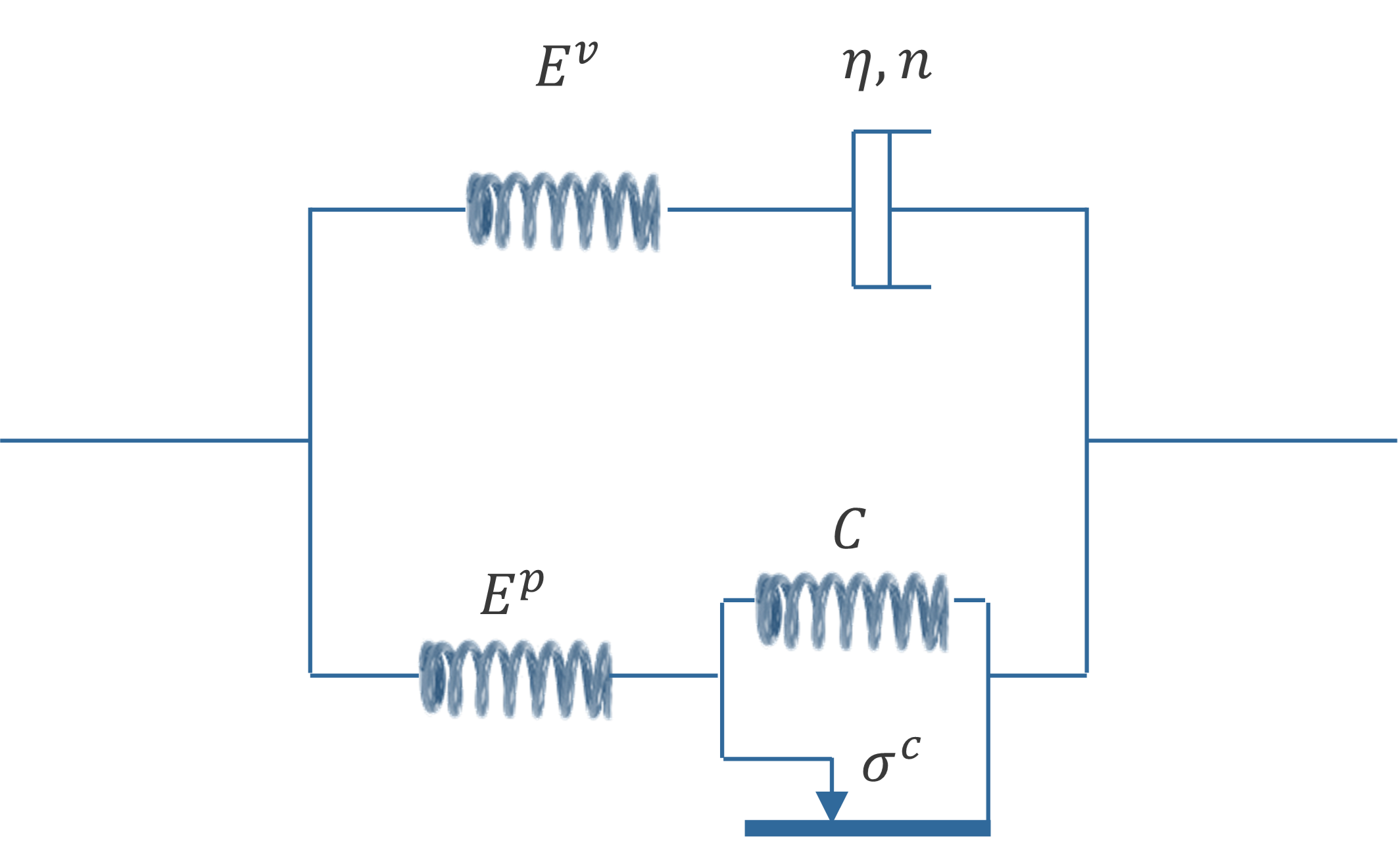
_images/1000020100000851000005193D8DB6B3DA4B1F95.png

1.2. Material parameters#

The behavioral relationship is based on nine parameters, which are characteristics of the material in question:

  • the Young’s modulus \({E}^{p}\) and the Poisson’s ratio \({\nu }^{p}\) of the elastoplastic branch, defined under the keyword factor ELAS (E, NU) of the command DEFI_MATERIAU;

  • The elastic limit \({\sigma }^{c}\) and the Prager constant \(C\) (without corrective factor 2/3), defined under the keyword factor KICHENIN_NL (SIGC and PRAGER) of the command DEFI_MATERIAU;

  • the Young’s modulus \({E}^{v}\) and the Poisson’s ratio \({\nu }^{v}\) of the viscoelastic branch, defined under the keyword factor KICHENIN_NL (E_ VISC and NU_VISC) of the DEFI_MATERIAU command;

  • the viscosity coefficient \(\eta\), the Poisson’s ratio \({\nu }^{d}\) and the nonlinearity exponent \(n\le 1\) of the shock absorber, defined under the keyword factor KICHENIN_NL (ETA_AMOR, NU_AMORet N_ AMOR) in the DEFI_MATERIAU command.

These parameters may depend on the temperature (keywords factor *_FO). The law of behavior is expressed in mechanical deformations, i.e. it is compatible with the usual shrinkage terms, in particular thermal deformation.

It is important to note that the stiffness defined under the keyword factor ELAS does not constitute all the (instantaneous) stiffness of the material but only that relating to the elastoplastic branch.

1.3. Internal variables#

The law of behavior is based on twelve physical internal variables: the components of plastic deformation \({\epsilon }^{p}\) (at the level of the pad of the elastoplastic branch) and of viscous deformation \({\epsilon }^{v}\) (at the level of the shock absorber of the viscoelastic branch). They are complemented by cumulative plastic deformation and cumulative viscous deformation.

EPSPEQ

V1

Cumulative plastic deformation

EPSPXX - EPSPYZ

V2- V7

Components of plastic deformation

EPSVEQ

V8

Cumulative viscous deformation

EPVXX - EPVYZ

V9- V14

Components of viscous deformation