1. Field of application#
1.1. Purpose#
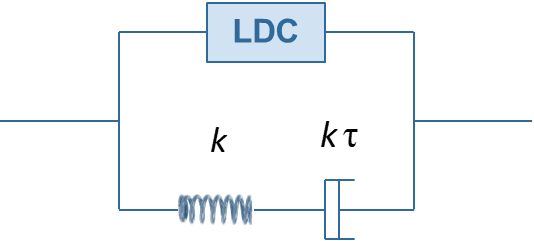
To regularize certain forms of quasistatic instabilities, a regularization technique accessible in STAT_NON_LINEvia the REGU_VISC keyword is based on the superposition of behavioral constraints with viscoelastic constraints, the latter being able to give the system the expected stabilization, see [Lorentz, Drouet, Hamon, 2020]. Subject to providing sufficient rigidity, the evolution of the solution then becomes continuous with respect to time and the division of the time step then again constitutes a response to possible convergence difficulties. Such a superposition is described in the figure below, where LDC represents the « true » law of material behavior and the Maxwell system of the lower branch corresponds to viscous stiffness. The law of behavior REGU_VISC_ELAS describes the behavior of this viscoelastic branch.
This behavior model is compatible with:
with a kinematics of small disturbances (HPP) or large deformations (GDEF_LOG);
with a local behavior law or with an internal variable gradient in which the gradient of an internal variable intervenes, see [Lorentz & Andrieux, 1999] or [R5.04.01].
1.2. Material parameters#
The viscoelastic model is based on two parameters: the stiffness of the spring noted \(k\) and the viscosity of the shock absorber. Rather than entering the latter, we prefer to introduce the time characteristic of the viscoelastic branch, noted \(\tau\). These parameters are entered under the keyword factor VISC_ELAS from the DEFI_MATERIAU command (keywords K and TAU).
1.3. Deformation measurements#
The behavior model is fed by mechanical deformation (i.e. without the terms of thermal shrinkage and others) if this is the case with the main law of behavior. Otherwise, it is the total deformation (the displacement gradient). Both PETIT and GDEF_LOG cutscenes are supported. Deformation \(\epsilon\) will be noted below, without loss of generality.
1.4. Internal variables#
The law of behavior introduces eight internal variables. On the one hand, these are the six components of stress in the viscoelastic branch, which accounts for the history effect of the model. And on the other hand, two additional variables are calculated essentially for post-processing purposes, to measure the extent of the viscous effects associated with regularization: these are the elastic volume energy stored in the spring and the volume energy dissipated by viscosity by the damper (accumulated over time).
The internal variables are grouped together in the following table. The corresponding indices do not correspond to the internal variable number; in fact, they are stored after the internal variables of the main law of behavior (if the latter relies for example on five internal variables, those related to viscoelastic regularization will be available under V6 to V13).
SIVXX - SIVYZ |
1 - 6 |
Components of viscous stress |
VISCELAS |
7 |
Stored elastic volume energy |
VISCDISS |
8 |
Volume energy dissipated by viscosity |