1. A few reminders on mechanical behavior

In mechanics, we can group under the term « law of behavior » the models that govern the relationship between local states of stress and deformation, possibly taking into account previous states.

Before talking about laws of behavior, it seems useful to us to quickly recall the main phenomena that can be encountered in terms of material behavior, with particular emphasis on the behavior of metallic materials.

In order to deepen the subject, the reader may refer to various reference books in the field, including [bib2] and [bib3].

1.1. Elasticity and plasticity

The simplest law of behavior is linear elasticity, which corresponds to the ability of the material to return to its original shape when the stress is removed. The law of behavior, which represents linear elasticity, corresponds to a relationship of proportionality between stresses and deformations. For a large number of materials, elasticity can be considered isotropic (the coefficient of proportionality is the same regardless of the direction of stress). However, some materials (monocrystals, textured materials) have different elastic characteristics depending on the direction of the stress.

Some materials such as elastomers have non-linear elastic behavior. In this case, the stresses and the deformations are no longer linked by a relationship of proportionality, however the material returns to its initial shape when it is not stressed.

For most materials (including metallic materials), linear elastic behavior is observed for moderate stresses. When the load is continued to increase, an irreversible plastic deformation is progressively created and the linearity relationship between stress and deformation is lost.

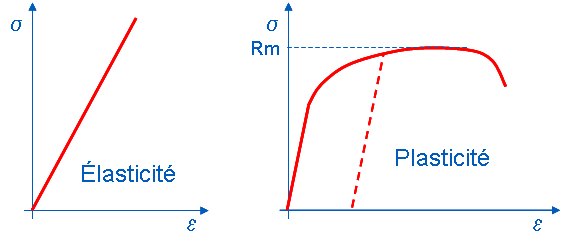
Figure 1.1-1: Elastic and plastic behaviors

1.2. Influence of temperature

When the same material is mechanically stressed at different temperature levels, an evolution of its response is observed both in the elastic domain and in the plastic field. Generally, when the temperature increases, the total deformation observed is greater for the same stress level.

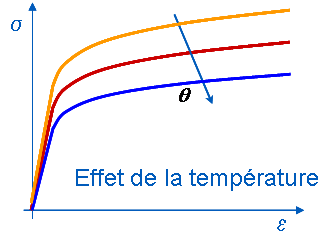
Figure 1.2-1: Influence of temperature

1.3. Viscosity

If the same material is used with different loading speeds, different mechanical responses are generally obtained in the plastic field. The sensitivity to the loading speed reflects the viscous nature of the material.

Viscosity occurs in different ways depending on the type of stress applied. With increasing monotonic loading, attention will be paid to the work hardening module as a function of the loading speed. It is also possible to apply a deformation step to the material and then observe the gradual decrease in the constant deformation stress. We then talk about relaxation. It is also possible to impose a stress level and observe a gradual increase in deformation at constant stress. We then speak of creep.

It should be noted that viscosity is generally a thermally activated mechanism. It will be all the more important if the material is at a high temperature. Sometimes more complex temperature dependencies can be identified. This is the case, for example, with austenitic stainless steels, which have a significant viscosity at room temperature. This viscosity decreases when the temperature increases and becomes practically zero around \(350°C\) then it reappears and increases rapidly beyond \(450°C\).

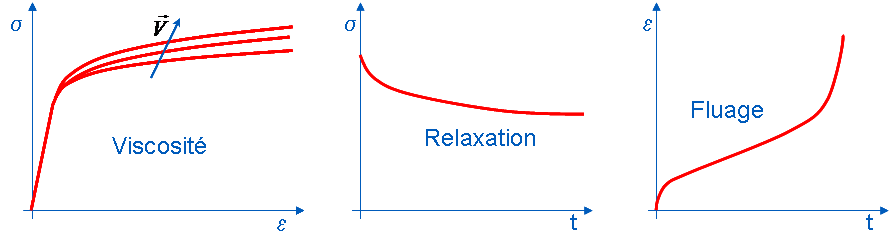
Figure 1.3-1: Manifestation of viscosity according to the nature of the stress

1.4. Cyclical behavior

The phenomena described so far can be observed with monotonic loads. When the stress applied is cyclical and the level of stress applied is sufficient to cause plastic deformation of the material, an evolution of the mechanical response is observed over the cycles. Depending on the material in question, this evolution may be of different types.

Under cyclic stress with a constant stress amplitude, an accumulation of deformation is observed during the first cycles. If the stress amplitude is high enough, deformation continues to accumulate with each cycle. We then speak of progressive deformation which can lead to the rapid breakage of the material.

If the magnitude of stress applied is more moderate, a stabilization of the cyclic response is observed. Depending on the material (and the loading amplitude) stabilization can be of two types. If the stabilized cycle has plasticity, we speak of material accommodation. If the stabilized cycle is completely elastic, this is called adaptation.

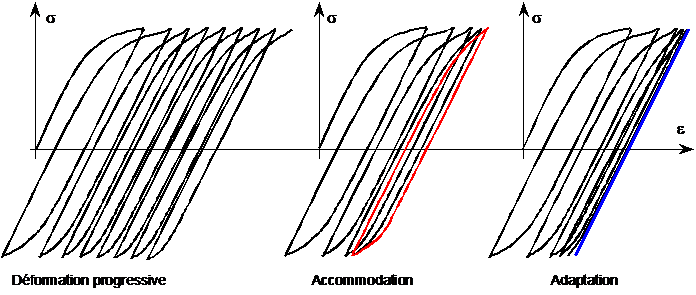
Figure 1.4-1: Stabilization of the cyclic response of the material

Under cyclic loading, a change in the envelope of the loading path is generally observed over the cycles due to an accumulation of work hardening. Materials can be classified into two categories:

1. Softening materials when the stress amplitude decreases for a loading with a constant amplitude of deformation, or when the amplitude of deformation increases for a loading with a constant amplitude of stress.

2. Materials that harden when the stress amplitude increases over the cycles for a loading with a constant amplitude of deformation or whose amplitude of deformation decreases for a loading with a constant amplitude of stress.

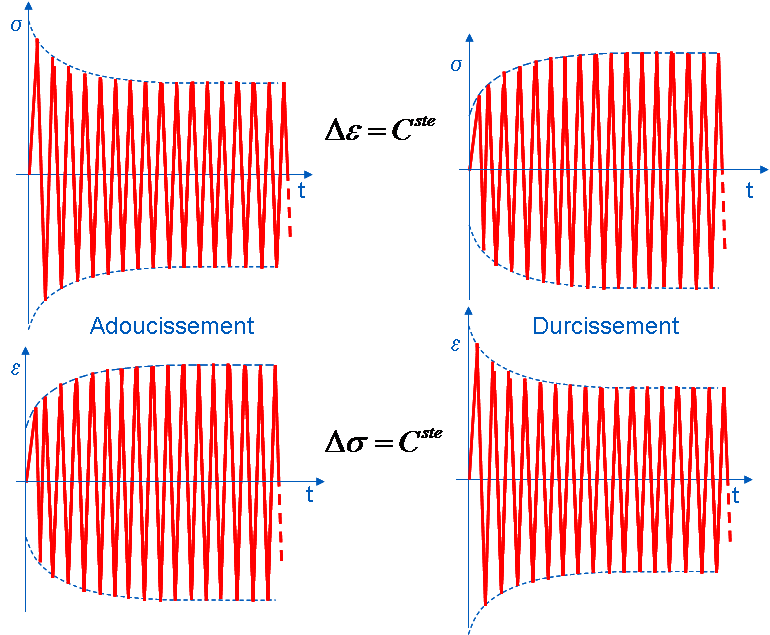
Figure 1.4-2: Cyclic Hardening and Softening

When the loading amplitude is constant, the phenomena of hardening or softening tend to dampen with the accumulation of cycles in order to achieve stabilization of the response of the material.

If the material has viscosity, the response of the material to cyclic loading will be dependent on the stress rate.

1.5. Static restore

Some materials are also sensitive to time in the case of loading with plasticization followed by unloading and then reloading. If the material is left to rest for a certain period of time before carrying out the second load, a restoration phenomenon is sometimes observed.

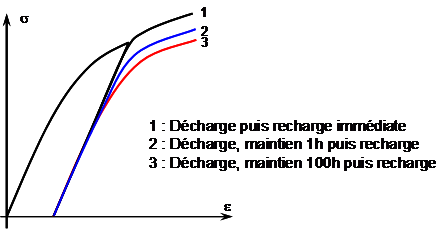
Figure 1.5-1: The restoration phenomenon

If the recharge is carried out immediately after the discharge, an elastic behavior is observed until the maximum stress level before discharge is reached, then the response curve of the material is in line with the initial curve before discharge.

If the material is sensitive to restoration, and if the material is left to rest before recharging it, a material response is observed that will be intermediate between the initial response of the material and the response obtained during an immediate recharge. It is therefore observed that the material at rest progressively loses the memory of the work-hardening accumulated during the first loading.

1.6. Memory effect

On certain metallic materials, and more particularly alloys with a crystalline structure \(\mathit{C.F.C.}\) (Cubic Face Centered), it is observed that cyclic behavior preserves the memory of the maximum deformation level reached during the life of the material.

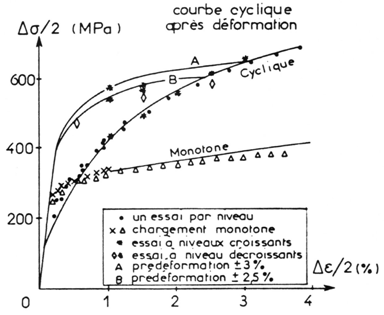
Figure 1.6-1: The memory effect of work hardening

Figure 1.6-1 describes the evolution of the stress amplitude as a function of the deformation amplitude for a large number of cyclic tests on the same material. When an initially virgin material is used, the cyclic consolidation curve shown on the diagram is obtained. If the material is first worked out to a relatively high level of deformation and then cycling with a lower loading, the response corresponds to a « harder » material as shown by the two curves A and B corresponding to different pre-work hardening levels.

1.7. Over-work hardening

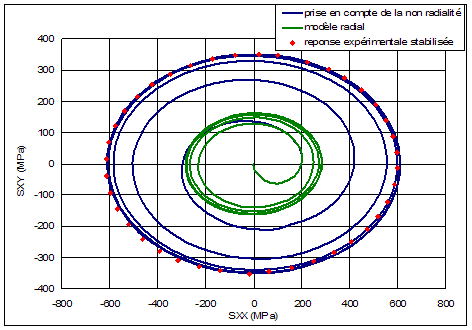
The mechanical response of the material can sometimes be very different depending on whether the load is uniaxial or whether it is multi-axial and non-proportional. We then speak of multi-axial over-work hardening. This phenomenon is illustrated by the following two figures. A 316L steel specimen is subjected to a loading process combining alternating traction and twisting (controlled in terms of deformation) with a phase difference of 90° between the two stresses.

The stress levels achieved (represented by the red dots on the right side of the figure) are approximately twice as high as those that would be achieved on a stressed specimen with a loading radial or uniaxial with an equivalent amplitude of deformation.

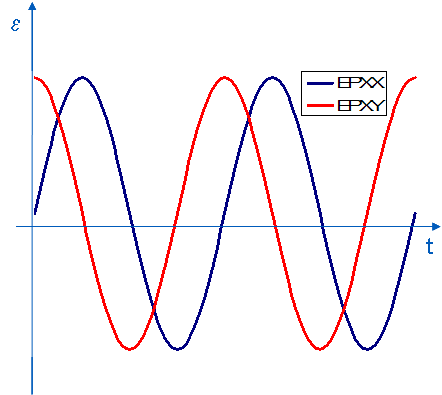
Figure 1.7-1: Over-work hardening effect under non-radial multiaxial loading

This test was simulated with two different laws of behavior. The blue curve corresponds to a behavior model capable of reproducing the effect of over-work hardening. The green curve is obtained with a similar law of behavior in which the consideration of over-work hardening has been removed. The second formulation predicts significantly lower stress amplitudes, which correspond to the response of the material for radial loading.

1.8. Isotropic and kinematic work hardening

When the loading exceeds the elastic limit of the material, we saw previously that plasticization is accompanied by work hardening which changes the subsequent response of the material in the event of alternating discharge or loading.

If we place ourselves in the stress space, we can define a threshold surface within which the material remains elastic. When the loading path reaches this surface, plastic deformation occurs and the threshold surface adapts in such a way that the charging point remains on the surface as long as there is no discharge. The load surface can be adapted in two distinct ways:

If the surface expands while remaining centered on the origin (which corresponds to a state of zero stress) we speak of isotropic work hardening (see Figure 1.8-1). Isotropic work hardening therefore corresponds to a variation in the size of the elastic domain.

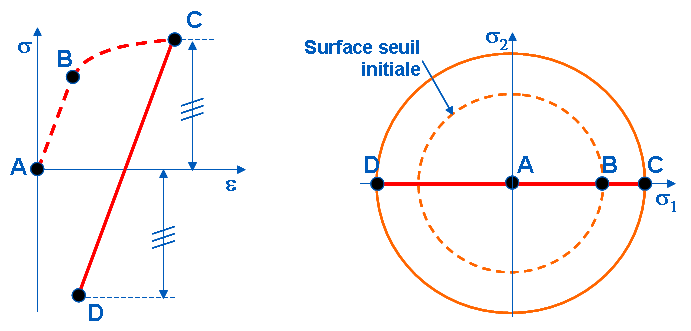
Figure 1.8-1: Isotropic work hardening

For a loading of traction followed by a discharge and then a compression, the material will maintain elastic behavior up to a level of compression equivalent to the maximum load achieved in traction.

If the load surface moves to follow the load we speak of kinematic work hardening (see Figure 1.8-2). The elastic domain maintains a constant size and is translated to follow the load. In the case of alternating tension-compression loading, the elastic domain will correspond to twice the initial elastic limit (in the absence of residual stress in the virgin material).

Figure 1.8-2: Kinematic work hardening

The behavior observed on real materials generally corresponds to a combination of kinematic and isotropic work hardening.