Bi-linear elastic behavior DIS_BILI_ELAS#
Definition#
Behavior DIS_BILI_ELAS is used to model reversible bilinear elastic behavior in translation, in each direction. The law of behavior was designed to be used with all discrete elements. The behavior is characterized by two slopes (KDEB and KFIN) and by effort (FPRE) which defines slope failure.
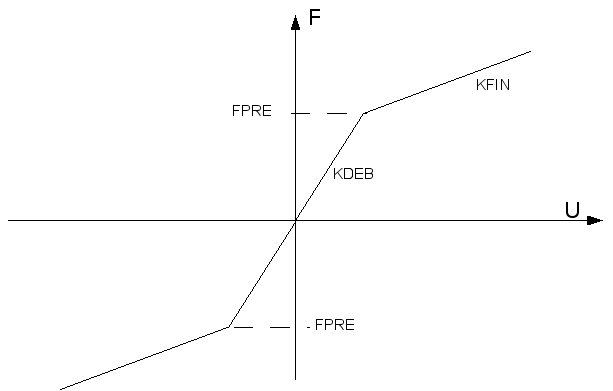
Bilinear elastic behavior.#
For this law, regardless of the degree of freedom considered, the behavior of the discrete is either elastic or elastic-bilinear. If in one of the directions the bilinear behavior is not defined, the behavior in this direction is then elastic and the values given in the AFFE_CARA_ELEM command are taken. Law DIS_BILI_ELAS only concerns the degrees of translation, so this implies that the behavior is elastic for the degrees of freedom of rotation that exist for this discrete. This local coordinate system is defined in the standard way in the AFFE_CARA_ELEM command under the ORIENTATION factor keyword.
The 3 characteristics (KDEB, KFIN, FPRE) are necessarily given in the local coordinate system of the element, it is therefore necessary in the command AFFE_CARA_ELEM under the key word factor DISCRET to specify REPERE =” LOCAL “. A fatal error is issued by*Code_Aster* if this condition is not met.
The quantities kdeb and kfin are functions that depend on temperature and can be defined as a function, sheet, or formula.
The incremental equations of the law of behavior are simply:
If \(∣F∣\le \mathrm{FPRE}\Rightarrow \mathrm{dF}=\mathrm{KDEB.}\mathrm{dU}\) If not \(\mathrm{dF}=\mathrm{KFIN.}\mathrm{dU}\)
\(F\) being the effort at the time \(t\) considered in one of the translation directions, and \(\mathrm{dU}\) the translational displacement increment in this direction.
Internal variables#
There is one « internal variable » per degree of translational freedom. It can take 3 values:
\(V1=0\), discretion has never been sought in this direction.
\(V1=1\), we are in the case where \(\mid F\mid \le \mathrm{FPRE}\)
\(V1=2\), we are in the case where \(\mid F\mid >\mathrm{FPRE}\)