Behavior DIS_CHOC_TRAC

Definition

Behavior DIS_CHOC_TRAC is an elastic nonlinear behavior that applies to the local DX degree of freedom of discrete elements with two nodes (mesh SEG2)

The non-linear behavior is given when defining material DIS_CHOC_ELAS by a \(F=\mathit{fonction}(\mathrm{\Delta }U)\) curve:

• \(\mathrm{\Delta }U\) represents the relative movement of the 2 nodes in the element’s local coordinate system.

• \(F\) represents the effort expressed in the element’s local coordinate system.

Data setting

Nonlinear function

A necessary data is the function describing the non-linear behavior. This function must meet the following criteria:

• It is a function in the sense of code_aster: defined with the operator DEFI_FONCTION,

• The interpolations on the x-axis and the y-axis are linear,

• The name of the abscissa when defining the function is DX,

• Extending to the left is excluded,

• The extension to the right of the function is either excluded or linear,

• The function must be defined by at least 2 points.

• The first point is \((\mathrm{0.0,}0.0)\) and must be given,

• The function must be strictly increasing,

The first two points of the function are used to define the elastic slope to the behavior. The x-axis and ordinate units should be consistent with those of the problem:

• the abscissa must be homogeneous when displaced,

• the ordinate (value of the function) must be homogeneous to an effort.

Definition of contact distance

++————————————————————————————————————————————————————————————————————————–+ ||In the case of a discrete with 2 knots: \(\mathit{DistanceContact}=\mathit{LongueurDiscret}–\mathit{dist}1–\mathit{dist}2\) The contact distance is positive in the direction of the local axis \(\mathit{Xloc}\).| ++————————————————————————————————————————————————————————————————————————–+

In the case of a discrete with 2 knots (based on a SEG2).

Let’s say two structures \({\Omega }_{1}\) and \({\mathrm{\Omega }}_{2}\). Note \({d}_{N}\) the normal distance between structures, \({F}_{N}^{1/2}\) the normal reaction force of \({\mathrm{\Omega }}_{1}\) over \({\mathrm{\Omega }}_{2}\).

In the coordinate system local to the element, the normal distance \({d}_{N}\) is expressed as:

\({d}_{N}=(({X}_{\mathit{loc}2}^{0}+{u}_{2})–({X}_{\mathit{loc}1}^{0}+{u}_{1}))–{\mathit{dist}}_{1}-{\mathit{dist}}_{2}\).

There will be « shock » when \({d}_{N}\le 0\)

The depression of the discrete will therefore be \(\Vert {d}_{n}\Vert\) and the effort will follow the given behavior curve.

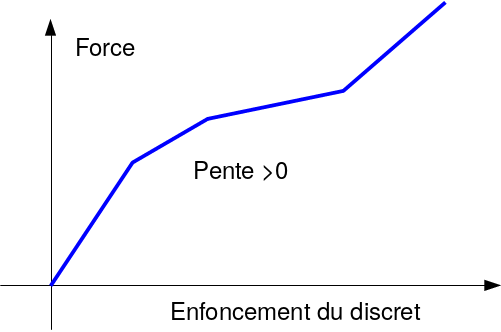
Function: Contact force vs indentation