4. Transformation plasticity#

Experimentally, it is observed that the dilatometric reading of a test piece during structural transformation is strongly influenced by the stress state and that the application of a stress even lower than the elastic limit of the material can nevertheless cause irreversible deformation (cf. [Figure 4-1]).

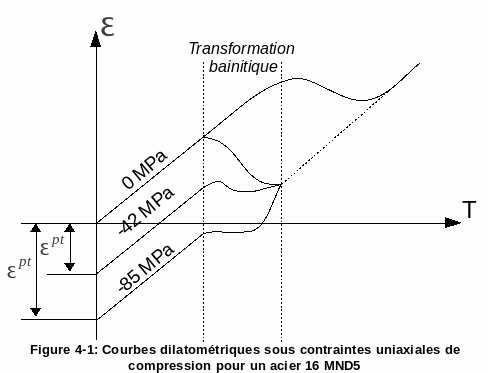
_images/Cadre2.gif

We call transformation plasticity this phenomenon and we note \({\varepsilon }^{\text{pt}}\) the corresponding irreversible deformation. The most frequently used transformation plasticity model was, originally, the three-dimensional generalization of the one-dimensional phenomenological model established by Desalos [bib7] _. If, on the basis of a dilatometric test, we draw the difference between the elongation \(\varepsilon\) obtained between the elongation obtained for an applied stress different from zero and that obtained for a zero stress as a function of the progress of the transformation, we note that:

(4.1)#\[ {\ varepsilon} ^ {\ text {pt}}} (\ sigma, b) =\ varepsilon (\ sigma, b) -\ varepsilon (\ mathrm {0,} b) =\ mathrm {0,} b) =\ mathrm {kF} (b)\ sigma\]

With:

\(k\):

Homogeneous constant in contrast to a constraint;

\(F\):

Normalized function (\(F(0)\mathrm{=}0\) and \(F(1)\mathrm{=}1\));

\(b\):

Proportion of the transformed phase;

A three-dimensional and temporal generalization of the previous experimental model, for a single transformation, was proposed by Leblond [bib8] _, [bib9] _, [bib10] _, [bib10] _, [bib11] _, in the form:

(4.2)#\[ {\ dot {\ varepsilon}} _ {\ mathit {ij}}} ^ {\ mathit {pt}}\ mathrm {=}\ frac {3} {2} K {\ tilde {\ sigma}}} K {\ tilde {\ sigma}}} _ {\ mathit {ij}}} _ {\ mathit {ij}}} F\ text {'} (b)\ dot {b}}\]

It is based on the following heuristic considerations:

  • The relationship must be « incremental », that is, relate the plastic deformation rate to the transformation rate;

  • The rate of plastic transformation deformation must be, as for classical plasticity, proportional to the deviatoric part \(\tilde{\sigma }\) of the strained tensor \(\mathrm{\sigma }\). Transformation plasticity occurs without a change in volume, resulting in a dependence on the stress deviator rather than on the stress field itself;

  • The transformation plastic deformation rate must be zero outside the transformation ranges;

  • The integration of this relationship in the uniaxial case with constant stress \(\sigma\) must restore the experimental relationship.

Based on experimental tests and for a bainitic type of transformation of a 16 MND5 steel for example \(K\mathrm{=}{10}^{\text{-4}}{\mathit{MPa}}^{\text{-1}}\) and \(F(b)=b(2-b)\).

The phenomenon of transformation plasticity can exist during structural transformations under ferritic, pearlitic, bainitic and martensitic stresses, which may possibly occur simultaneously. On the other hand, it is considered that this phenomenon does not exist during austenitic transformation. To simplify the writing, we note for the plasticity of transformation:

(4.3)#\[ {g} _ {Z} ^ {\ mathit {pt}}}\ left (Z,\ dot {Z}\ right) =\ sum _ {{k} _ {f} =1} ^ {4} {K} _ {K} _ {k} _ {k} _ {f}} {F}} _ {f}} _ {f}}} ^ {\ text {'}}}\ langle {\ dot {Z}} _ {Z}} _ {k} _ {f}}\ rangle\]

So the general model implemented in*code_aster* is:

(4.4)#\[ {\ dot {\ epsilon}}} ^ {\ mathit {pt}}}\ left (\ sigma, Z\ right) =\ sum _ {{k} _ {f} =1} ^ {4} {\ dot {\ epsilon}} {\ dot {\ epsilon}}}}\ left (\ dot {\ epsilon}} {4} {\ dot {\ epsilon}}} {\ dot {\ epsilon}}} {\ dot {\ epsilon}}}} {\ dot {\ epsilon}}}\ left (\ dot {\ epsilon}}} {\ dot {\ epsilon}}} {\ dot {\ epsilon}}}} {\ dot {\ epsilon}}} {\ dot {\ epsilon}}}\ 2}\ stackrel {} {\ sigma} {\ sigma} {g} {g}} _ {Z} ^ {\ mathit {pt}}\ left (Z,\ dot {Z}\ right)\]

Where \(\mathrm{\langle }X\mathrm{\rangle }\) refers to the positive part of a quantity. In code_aster, it is possible not to take into account the phenomenon of transformation plasticity. If this phenomenon is taken into account, it appears as soon as there is transformation, even if the structure plasticizes. The model is more particularly dedicated to steel. Data \({K}_{{k}_{f}}\) and \({F}_{{k}_{f}}^{\text{'}}\) are provided by the user in DEFI_MATERIAU under the keyword META_PT.

Physical parameter for transformation plasticity

Keyword META_PT

Constant for ferritic phase 1

\({K}_{1}\)

F1_K

Constant for ferritic phase 2

\({K}_{2}\)

F2_K

Constant for ferritic phase 3

\({K}_{3}\)

F3_K

Constant for ferritic phase 4

\({K}_{4}\)

F4_K

Derived function for ferritic phase 1

\({F}_{1}^{\text{'}}\)

F1_D_F_ META

Derived function for ferritic phase 2

\({F}_{2}^{\text{'}}\)

F2_D_F_ META

Derived function for ferritic phase 3

\({F}_{3}^{\text{'}}\)

F3_D_F_ META

Derived function for ferritic phase 4

\({F}_{4}^{\text{'}}\)

F4_D_F_ META