2. Under integration of QUAD4#
Despite all the potential of the isoparametric quadrilateral element for finite element calculation, the application of a classical bilinear formulation to define its field of displacement leads to poor results. There are various reasons for this:
it has excessive rigidity (« lock »), during a load in which the plane bending part is important.
the classical bilinear formulation of the displacement field is very sensitive to mesh distortion and presents severe « locking » when applied to an incompressible material.
One solution to these numerical blocking problems consists in calculating the stiffness matrix by means of reduced integration. The principle of this method is to consider fewer integration points during the numerical integration diagram than are usually needed to evaluate the exact stiffness matrices of the element. Starting from the isoparametric element QUAD4 [R3.03.02], we modify the number of integration points as well as the weight and coordinates of these points, to create the sub-integrated element that we will name in this document: QUAS4
QUAS4
QUAD4
Number of integration points: 4 |
Number of integration points: 1 |
|
Weight of each point: 1 |
Weight of the point: 4 |
|
Coordinates: \((x,y)\mathrm{=}(\mathrm{\pm }\frac{1}{\sqrt{3}},\mathrm{\pm }\frac{1}{\sqrt{3}})\) |
Coordinates: \((x,y)\mathrm{=}(\mathrm{0,0})\) |
2.1. Formulation#
At the center, the discretized gradient operator used to calculate the stiffness matrix is of the following form:
\(B={B}_{c}=\left[\begin{array}{cc}{b}^{{t}_{x}}& 0\\ 0& {b}^{{t}_{y}}\\ {b}^{{t}_{y}}& {b}^{{t}_{x}}\end{array}\right]\) eq 2.1-1
With
\(\begin{array}{}{b}_{x}^{t}=N,x(0)=\frac{\partial N}{\partial x}\mid \xi =\eta =0\\ {b}_{y}^{t}=N,y(0)=\frac{\partial N}{\partial y}\mid \xi =\eta =0\end{array}\) eq 2.1-2
and \(N\) represents \(({N}_{1},{N}_{2},{N}_{3},{N}_{4})\), the vector of shape functions. Recall that vectors \(b\) represent the simplest form of the discretized under-integrated gradient operator introduced by Hallquist [bib1] and which is based on the evaluation of the derivatives of the isoparametric form functions at the origin of the coordinate system \((\xi ,\eta )\)
That is:
\(\begin{array}{c}{b}_{x}^{t}\mathrm{=}\frac{1}{\mathrm{2A}}\left[({y}_{2}\mathrm{-}{y}_{4}),({y}_{3}\mathrm{-}{y}_{1}),({y}_{4}\mathrm{-}{y}_{2}),({y}_{1}\mathrm{-}{y}_{3})\right]\mathrm{=}\text{Constant sur l'élément}\\ {b}_{y}^{t}\mathrm{=}\frac{1}{\mathrm{2A}}\left[({x}_{4}\mathrm{-}{x}_{2}),({x}_{1}\mathrm{-}{x}_{3}),({x}_{2}\mathrm{-}{x}_{4}),({x}_{3}\mathrm{-}{x}_{1})\right]\mathrm{=}\text{Constant sur l'élément}\end{array}\) eq 2.1-3
\(A\mathrm{=}(1\mathrm{/}2)\text{.}((\mathit{x2}\mathrm{-}\mathit{x4})\text{.}(\mathit{y3}\mathrm{-}\mathit{y1})+(\mathit{x3}\mathrm{-}\mathit{x1})\mathrm{\ast }(\mathit{y4}\mathrm{-}\mathit{y2}))\): Area of the element
The stiffness matrix is written as:
\({K}_{e}\mathrm{=}{K}_{c}\mathrm{=}A\text{.}{B}_{{c}^{T}}\text{.}C\text{.}{B}_{c}\) eq 2.1-4
\(C\) being:
is the elastic behavior matrix for elasticity calculations
is the tangent matrix for plasticity calculations. Note that during such calculations, it is the integration of the law of behavior at the Gauss point (at the center in our case) that determines the value of the coefficients of \(C\).
Finally, internal forces are written as:
\({F}_{\text{int}}\mathrm{=}{K}_{e}\text{.}U\mathrm{=}{B}_{{c}^{T}}\text{.}{\sigma }_{c}\) eq 2.1-5
\(U\): Vector of nodal movements.
2.2. Calculation failed in Code_Aster: parasitic modes#
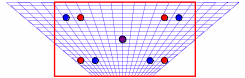
The calculations launched on test case No. 1 with such an element fail. The calculation step of inverting \({K}_{e}\) to determine the nodal displacements cannot be completed. In fact, at the center, the stiffness matrix is singular. By displaying the core of \({K}_{e}\), we see that its dimension is no longer three but five. Two vectors were added to the core and made the inversion of the stiffness matrix impossible. The appearance of these two additional vectors in the core of \({K}_{e}\) is directly linked to the fact that we choose the center as the only point of integration. In other words, there are two nodal displacement fields other than the displacement fields corresponding to rigid solid motion cancelling out internal forces. These modes represent the hourglass modes of QUAD4 [Figure 2.2-a]. Subsequently, one of the stabilization steps will consist in enriching the discretized gradient operator in order to make \({K}_{e}\) invertible.

Figure 2.2-a