5. Thermal calculation of a cylinder subjected to a cold shock#
We illustrate on a numerical example what was shown previously; namely that diagonalization is effective in verifying the principle of the maximum.
We are inspired by the industrial example of the cooling of a molded elbow: a cold thermal shock (\(289°C\) to \(20°C\)) is applied to a cracked elbow. During the cooling transition, the temperature calculated at some nodes reaches \(310°\) without diagonalizing the mass matrices. For the example treated here, we restrict ourselves to a hollow cylinder of the same dimension as the elbow on which a cold thermal shock is applied.
5.1. Data#
We study a hollow cylinder that is supposed to be infinite. As there is no dependence on \(z\) (infinite cylinder), we limit the study to a plane calculation. For reasons of symmetry, only a portion of the structure is meshed.
Point coordinates:
\(x\) (\(\mathrm{mm}\)) |
\(y\) (\(\mathrm{mm}\)) |
\(z\) (\(\mathrm{mm}\)) |
|
\(\mathrm{M1}\) |
436.75 |
||
\(\mathrm{M2}\) |
|
|
The calculations are carried out on a linear mesh (cells TRIA3 - QUAD4):
Mesh characteristics:
Number of knots: \(90\)
Number and type of meshes: \(64\text{TRIA3}\mathrm{,32}\text{QUAD4}\)
Material characteristics:
\(\lambda =\mathrm{19,97}\text{W/m °C}\)
\(\rho \mathrm{Cp}=4.89488{10}^{6}{\text{J/m}}^{3}\text{°C}\)
Limit conditions and loading:
To ensure invariance by rotation, zero heat flow conditions are imposed on faces \(\mathrm{AB}\) and \(\mathrm{CD}\). The external wall is assumed to be perfectly insulated. On the inner skin \(\mathrm{AD}\), the heat transfer between the cylinder and the fluid is modelled by a high convective exchange coefficient:
\(h=40000\text{W/m² °C}\).
The cold thermal shock applied to the molded elbows is represented by a linear variation in the temperature of the fluid flowing in the pipe: \(289°\to 20°\) in \(\mathrm{12s}\). In order to accentuate the problem of exceeding the maximum and therefore to better highlight the influence of diagonalization, we adopt a more brutal shock: \(289°\to 20°\) in \(\mathrm{1s}\).
Discretization is adopted in the following time:
from \(t=0s\) |
to \(t=10s\), |
1 time step |
from \(t=10s\) |
to \(t=11s\), |
2 steps of time |
from \(t=11s\) |
to \(t=25s\), |
7 steps of time |
from \(t=25s\) |
to \(t=60s\), |
10 steps of time |
Numerically, the value selected for the time discretization parameter is \(\theta =\mathrm{0,57}\).
5.2. Results#
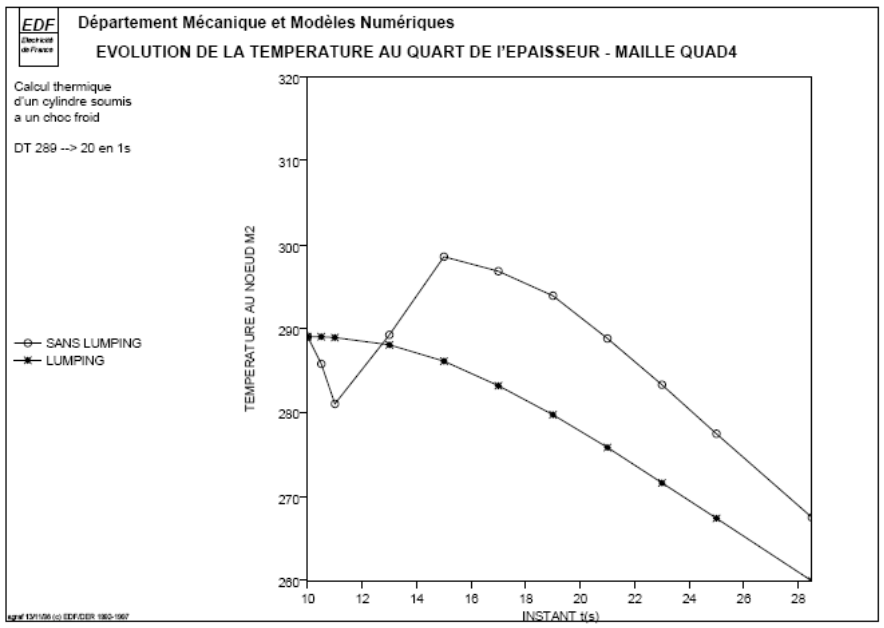
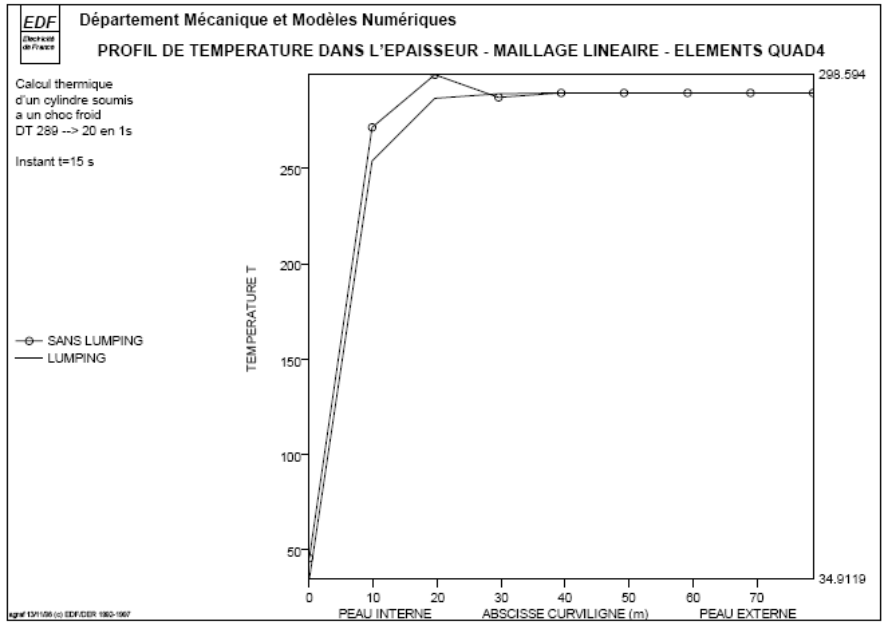
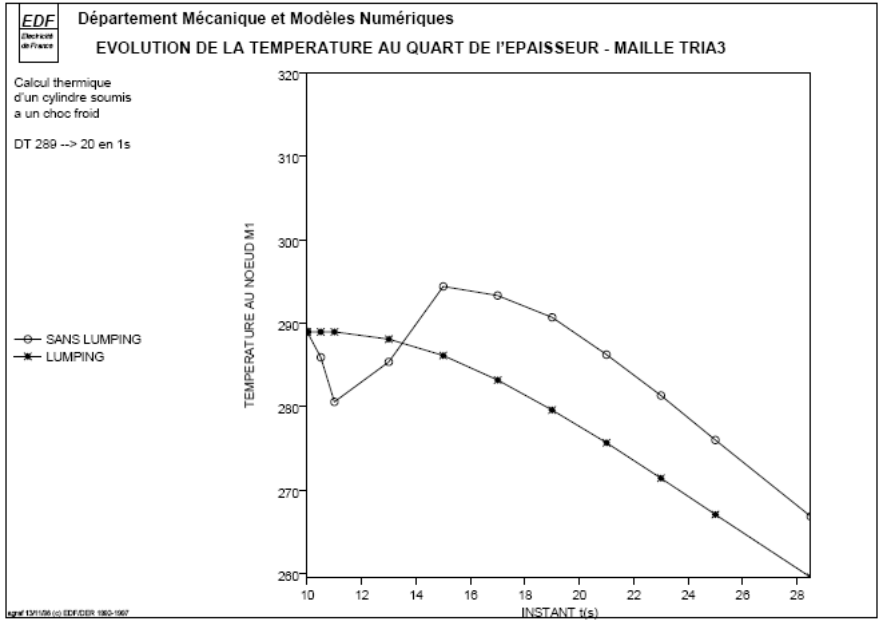
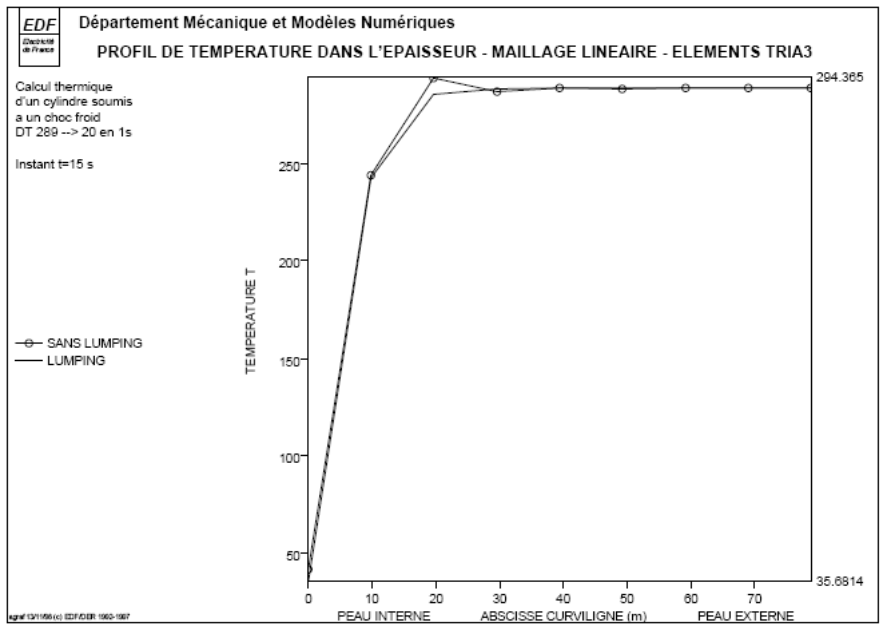
The following figures show the temperature profiles in the thickness of the cylinder at time \(t=\mathrm{15s}\) (the moment when the maximum exceeds the maximum are the greatest) without diagonalizing the mass matrices.
We also give the temporal evolution \(T(t)\) at the nodes \({M}_{1}\) and \({M}_{2}\) located at a quarter of the thickness of the inner skin.
Without diagonalization, we note that the temperature oscillates in time and space beyond the maximum value of \(289°\) at the beginning of the transient.
With diagonalization on the linear elements, a regular solution is observed without exceeding the maximum.
A similar study was conducted on 3D linear elements (tetrahedron with 4 knots, pentahedron with 6 knots, hexahedron with 8 knots). The results lead to the same conclusions: with diagonalization, the temperature oscillations disappear for the calculation on 3D linear elements.
Additional note concerning the thermo-mechanical calculation:
Another study was carried out in [bib1] to estimate the consequences of thermal diagonalization on mechanical results. It can be seen that the calculation ISO -P2 (quadratic elements divided into linear elements, whose mass matrices are lumped) provides satisfactory results. Spatial temperature oscillations are eliminated. But in the case studied, with a relatively coarse mesh, the mechanical solution remains imprecise. Although the thermal solution is correct, to improve the solution in terms of constraints, it is necessary in any case to refine the mesh.
For mesh TRIA3, diagonalization leads to a regular solution without exceeding the maximum:
For mesh QUAD4, diagonalization leads to a regular solution without exceeding the maximum: