3. Finite element method#
3.1. General principles#
The search for an appropriate approximate function across the entire domain becomes difficult in the general case of geometry of any shape. The idea of the finite element method is therefore to build this approximation in two stages:
Identify geometrically simple \({\Omega }_{e}\) sub-domains that tile the domain;
Define an approximate function on each sub-domain;
A certain number of characteristics of this construction are therefore apparent:
The paving of domain \({\Omega }_{e}\) by sub-domains \({\Omega }_{e}\) should be as accurate as possible;
The function approximated on the sub-domain must respect conditions of continuity between the various sub-domains;
The function approximated on the sub-domain must have properties consistent with the differentiability conditions and in relation to the physical description of the solution (which may involve using a weakened formulation for example).
3.2. Geometry approximation#
3.2.1. Principle#
We identify the \({N}_{e}\) subdomains (or elements) \({\Omega }_{e}\) that pave the \(\Omega\) space of the solid:
Note \({x}_{\alpha \mathrm{=}\mathrm{1,3}}\) the coordinates of a point \(x\) in the absolute coordinate system. The geometry of the subdomain is constructed with a nodal approximation, i.e. for an element with \({N}_{\mathrm{nd}}\) nodes:
This paving (meshing) is an operation that can be complex, especially in 3D. There are general algorithms for meshing. We use triangles or quadrangles in 2D and tetrahedra or hexahedra in 3D (plus a few elements that serve as connectors). Triangles and tetrahedra give what we call free meshes, quadrangles and hexahedra form adjusted meshes. Free meshes are relatively easy to build using widely proven techniques: Voronoï cells building a Delaunay triangulation or propagation methods (so-called frontal methods), controlled meshes are much more difficult to generate. The mesh necessarily induces a geometric discretization error. For example, in figure (), we see that a curved border is only imperfectly approximated by linear elements.

Illustration 1: Geometric discretization error |
Likewise, the mesh must be consistent: no holes or overlaps (see figure ()).
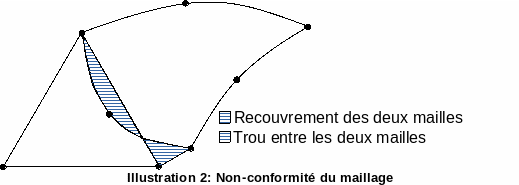
Illustration 2: Non-compliance of the mesh |
To respect this condition of compliance, two rules are sufficient:
Each element must be uniquely defined using the coordinates of its geometric nodes (and not those of its neighbors!) ;
The border of an element must be uniquely defined from the nodes of these borders, these nodes being common between the elements sharing this border.
These compliance conditions are an important difference from finite volumes that do not have these requirements. Domain tiling makes it possible to apply the finite element method to complex geometries, unlike finite difference methods. The geometric tiling of the domain induces a first error: it is not possible, in the general case, to represent real geometry by a mesh by regular polygons, in particular on the border of the domain.
« A good mesh is a good mesh »
3.2.2. Reference elements#
Calculating shape functions for any element can be quite complicated. This is why we often prefer to reduce ourselves to a so-called reference element, from which we can generate all the elements of the same family by a geometric transformation. The shape functions are then calculated on this generic element noted \({\Omega }_{r}\), and the transport of the quantities onto the real element \({\Omega }_{e}\) is carried out thanks to the knowledge of the geometric transformation.
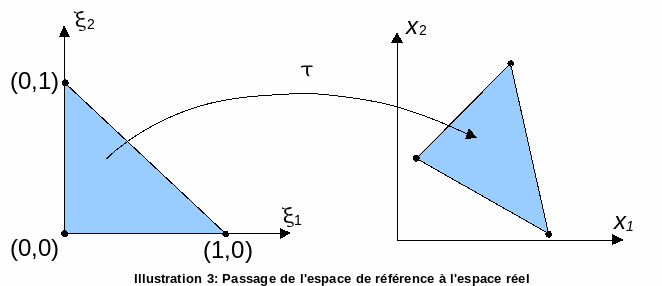
Illustration 3: Transition from reference space to real space |
The reference element points will be described in terms of parametric coordinates \({\xi }_{\alpha =\mathrm{1,3}}\). The \(\tau\) transformation should be bijective and transform the vertices and sides of the reference element into the vertices and sides of the real element:
3.2.3. Geometric interpolation functions#
The geometry of the element is therefore approximated by means of geometric interpolation functions. These functions noted \(\stackrel{ˉ}{N}(\xi )\) are defined on the reference element; they allow to know the coordinates \({x}_{\alpha }\) of any point of the real element from its coordinates \({\xi }_{\alpha }\) of its antecedent in the reference element and the coordinates \({x}_{\alpha }^{i}\) of the nodes (with a local number \(I\)) of the real element to be known:
3.2.4. Jacobian transformation matrix#
The Jacobian transformation is the matrix of the partial derivatives of the real coordinates \({x}_{\alpha }\) with respect to the coordinates \({\xi }_{\alpha }\) in the reference element:
Taking into account the definition of coordinates \({x}_{\alpha }\) according to the coordinates \({x}_{\alpha ,i}\) of the nodes, we obtain an equivalent expression of the Jacobian matrix:
Where \(\frac{\partial \stackrel{ˉ}{{N}_{i}}}{\partial {\xi }_{\beta }}\) are the terms in the \({\left[\frac{\partial \stackrel{ˉ}{N}}{\partial \xi }\right]}^{T}\) matrix, where the number of rows is the number of directions in space, and the number of columns is the number of nodes in the element. Note that the \({\left[\frac{\partial \stackrel{ˉ}{N}}{\partial \xi }\right]}^{T}\) matrix only depends on the definition of the reference element and not on the definition of the real element. The determinant of the Jacobian matrix, useful in the calculations that follow, is called the Jacobian of geometric transformation. It is non-zero when the \(\tau\) transformation that makes it go from the reference element to the real element is bijective, and positive when \(\tau\) respects the orientation of the space.
3.3. Representation of the unknowns#
To solve the problem, we consider a finite element approximation of an unknown field. Spaces \({E}_{P}\) and \({E}_{u}\) are represented by discrete spaces \({E}^{h}\). There are two equivalent ways to represent the unknowns in an element: by the coefficients of their polynomial approximation, or by their nodal values. These two possibilities correspond to the two complementary ways of defining an element: by the data of a monomial base, or by the data of the shape functions associated with the nodes. In general, the approximate function is constructed by writing the following linear relationship on each element:
Where \({\phi }_{i}^{e}(\xi )\) are independent linear functions. They form the basis of the approximation, the general parameters of the approximation being the coefficients \({a}_{i}\).
3.3.1. Nodal approximation#
The first idea of the finite element method is to build a nodal approximation for which the coefficients \({u}_{i}={a}_{i}\) correspond to the solution at these nodes:
We then obtain a nodal approximation with \({N}_{i}^{e}(\xi )\) the interpolation functions on the reference element. On each of these sub-domains, an approximate function is constructed that is different from one sub-domain to another. The finite element approximation is*elementary* because the function only depends on the nodal values that make up the element:
An element is isoparametric when it is based on identical interpolations for its geometry and unknowns: \(\stackrel{ˉ}{N}(\xi )=N(\xi )\).
To ensure the continuity of the solution on the element and, possibly, the continuity of its derivatives, it is necessary for the \({N}_{i}^{e}(\xi )\) functions to be continuous and, possibly, to have continuous derivatives.
Likewise, if we want to ensure the continuity of the solution and its derivatives at the boundaries of the elements (conformity of the approximation), the solution and its derivatives must depend in a unique way on the nodal variables of the nodes of the border.
3.3.2. Polynomial base#
The easiest way to define an element is to choose a polynomial base composed of a number of independent monomials. For a given unknown, the number of monomials used must be equal to the number of nodal variables, i.e. the number of nodes used to represent the unknown. The polynomial base is generally defined on the reference element; it contains monomials of the form \({\xi }_{1}^{\gamma }\mathrm{.}{\xi }_{2}^{\delta }\mathrm{.}{\xi }_{3}^{\varepsilon }\), where \(\gamma\), \(\delta\), and \(\varepsilon\) are positive or zero integer exponents. The degree of such a monomial is the integer \(\gamma +\delta +\varepsilon\). The base is said to be complete with degree \(n\) when all the monomials of degree \(n\) are present. In some cases, incomplete databases are used. We note \({P}_{p}(\xi )\) the \({p}^{\mathit{ième}}\) monomial of the base (which includes \(m\)). The components of the displacement vector \(u(\xi )\) in the element are then given by the formula:
Note \(\Pi\) the matrix giving the values taken by the monomials of the polynomial base on the nodes of the reference element:
where \(p\) is the order number of the monomial in the base, \(I\) is the node number locally to the element, and \({\xi }_{I}\) is the coordinate of the node \(I\) in the reference element. This matrix is square, its dimension is the square of the number of nodes in the element.
At node \(I\) the move \({u}_{\alpha }^{I}\) is equal to:
There are three main types of finite elements that are frequently used:
Lagrange finite elements, which are based on complete polynomial bases and various types of geometries (symplectic for triangles and tetrahedra, with a tensor structure for quadrangles and hexahedra, or prismatic);
Serendip-type finite elements, which are Lagrange finite elements with incomplete bases;
Hermite finite elements, of high precision, which use nodal unknowns and their derivatives;
Symplectic Lagrange finite elements
To determine if a polynomial base is complete with symplectic elements, simply use Pascal’s triangle:
A complete polynomial base of order two has six monomials: \(\mathrm{\{}1;{\xi }_{1};{\xi }_{2};{\xi }_{1}^{2};{\xi }_{2}^{2};{\xi }_{1}\mathrm{.}{\xi }_{2}\mathrm{\}}\) and therefore the supporting geometric element will be a triangle with six nodes.
Lagrange finite elements with tensor structure
To describe quadrangular (or hexahedral) finite elements, simply take complete polynomials of the given order and make them the product.
Order |
Constant |
Linear |
Quadratic |
Cubic |
|
Constant |
\(1\) |
|
|
|
|
Linear |
\({\xi }_{2}\) |
|
|
|
|
Quadratic |
\({({\xi }_{2})}^{2}\) |
|
|
|
|
Cubic |
\({({\xi }_{2})}^{3}\) |
|
|
|
A « over » -complete polynomial base of order two for a quadrangular element has nine monomials: \(\{1\text{;}{\xi }_{1}\text{;}{\xi }_{1}^{2}\text{;}{\xi }_{2}\text{;}{\xi }_{2}^{2}\text{;}{\xi }_{1}\mathrm{.}{\xi }_{2}\text{;}{\xi }_{1}\mathrm{.}{\xi }_{2}^{2}\text{;}{\xi }_{1}^{2}\mathrm{.}{\xi }_{2}\text{;}{\xi }_{1}^{2}\mathrm{.}{\xi }_{2}^{2}\}\), which means nine nodes. Such an element includes terms of order 3 and 4.
Serendip finite elements
Serendip elements, for a polynomial of order \(s\), exclude cross terms of degree greater than \(s+1\) for not having nodes inside the elements. For example, for a second-order Serendip element, the monomials will be \(\mathrm{\{}1\text{;}{\xi }_{1}\text{;}{\xi }_{1}^{2}\text{;}{\xi }_{2}\text{;}{\xi }_{2}^{2}\text{;}{\xi }_{1}\mathrm{.}{\xi }_{2}\text{;}{\xi }_{1}\mathrm{.}{\xi }_{2}^{2}\text{;}{\xi }_{1}^{2}\mathrm{.}{\xi }_{2}\mathrm{\}}\), which is eight nodes.
3.3.3. Shape functions#
An equivalent way to define a finite element is to give, for each unknown, the expression of the shape functions of the element. For a given scalar unknown (component of the displacement along y for example), there are as many as there are nodes where the unknown must be calculated. In many cases, the same shape functions are used for all components of an unknown vector, but this is not a mandatory step. In what follows, however, to simplify the entries, it will be assumed that this is the case.
The shape functions can be defined on the real element \({\Omega }_{e}\): they are then denoted \({N}^{e}(x)\), they depend on the geometry of the real element, and are therefore different from one element to another. It is easier to express them on the reference element, which gives the \(N(\xi )\) functions independent of the geometry of the real element. Recall that these functions are polynomial on the element, and that the form function associated with a given node takes the value one there, while it is canceled at all the other nodes of the element. The unknowns are then expressed as a linear combination of shape functions, the coefficients \({u}_{\alpha ,i}\) of the combination being called the nodal variables:
Using the \(\tau\) transformation between the reference element and the real element:
We have:
3.3.4. Correspondence between polynomial bases and form functions#
We have two relationships. The first comes from approximating the solution using a polynomial base:
The second is the nodal approximation:
The matrix giving the values taken by the monomials of the polynomial base on the nodes of the reference element:
In node \(I\), we wrote the following polynomial approximation;
By injecting equation () into the nodal expression (), we get:
By comparison with the polynomial approximation (), we deduce the following relationship between the polynomial base and the shape functions:
In practice, we will find in the literature the writings of the nodal form functions for the most common elements, according to the choice of the polynomial base.
3.4. Existence and uniqueness results#
The problem can be written more abstractly:
\({E}_{u}\) and \({E}_{v}\) are vector spaces of functions defined to \(\Omega\). They are Hilbert spaces.
\(a(\mathrm{u},\mathrm{v})\) is a bilinear form over \({E}_{u}\mathrm{\times }{E}_{v}\) (we assumed that \(\mathrm{L}(\mathrm{u})\) represents a linear physical problem with respect to \(\mathrm{u}\)).
\(f(\mathrm{v})\) is a linear and continuous form over \({E}_{v}\).
To establish the conditions of existence and uniqueness, the Lax-Milgram theorem is applied. At first, we assume that the solution belongs to the same space as the test functions \({E}_{u}\mathrm{=}{E}_{v}\)
If the form \(a(\mathrm{u},\mathrm{v})\) is coercive, that is to say:
So the problem:
Admits one and only one solution.